In this tutorial we shall solve another classical DP problem.
This problem is bit complex to understand. Hence first we shall solve this problem with help of recursion. Later we shall see how to solve it using DP.
Problem Statement:
You are given “n” floors and “m” eggs. You need to find from which floor the egg breaks with minimum number of throws.
Assumptions:
- If an egg breaks from floor “n”, the egg will break from all the floors above it.
- If an egg will not break from a floor n, then it will not break, if the egg is thrown from lower floors from “n”.
We shall understand the above problem with below points.
For example, you have 6 floors and 1 egg.
You cannot go directly to 6th floor and throw the egg and check if it breaks or not. Because, if the egg breaks, you cannot know if the egg breaks at floor 5 or not.
Hence we start from floor 1, and throw the egg. If it breaks, we mark as from the first floor egg breaks.
If the egg did not break then we shall throw the egg from 2nd floor, if the egg did not break, we go to 3rd will do this till we reach 6th floor.
So here in the worst case, we need to throw the egg “n” times.
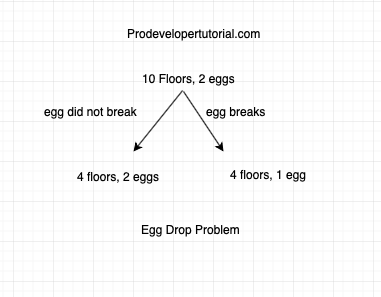
Suppose if you have 10 floors and 2 eggs. Then you can throw the egg from 5th floor. If the egg breaks, the number of eggs will be 1 and number of floors to check will be 4. Because we already know that the egg will break from 5th floor. So according to our assumption, the egg will break from the above floors also. Hence we need to check the floors below it.
If the egg did not break from floor 5, then we still have 2 eggs and we have 4 floors above to check. Why 4 floors?
Because 10 -5 -1 = 4.
We already know that the egg breaks from 5th floor, this can be represented as
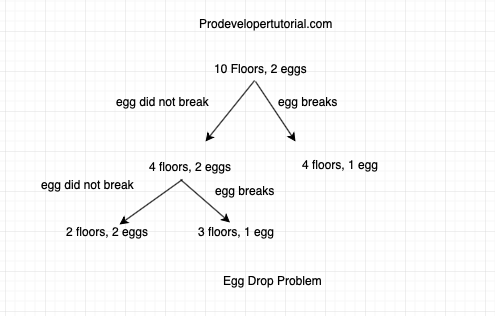
Again if we throw the egg from 3rd floor, if it breaks we have 1 egg, or if the egg didn’t break, we check from floor 2 with 2 eggs with us.
We can write a recursive formula as below:
egg_drop(n)
for i = 1 to no_of_floors
temp = 1 + max( egg_drop(egg-1, i-1), egg_drop(egg, floor-i))
Finally when the program iterates through all the floors from 1 to n, the min value in temp will be the answer.
In the formula, we added 1 because, we already used 1 try while throwing from a particular floor.
We use egg_drop(egg-1, i-1) because, we assume that the egg broke and hence we have 1 less egg.
We use egg_drop(egg, floor-i) because the egg did not break from that floor and need to check the floor above.
Now we shall see how to solve this problem with the help of DP.
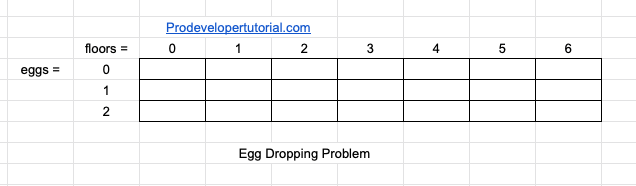
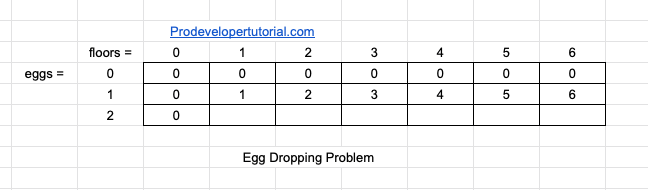
Suppose we have 6 floor and 2 egg, our DP array will be as below:
Here in DP, it is always good to start with 0 as it will be helpful to solve the problem further.
- In the DP array, we shall fill with the min num of tries. At the end we get the min number of tries to check from which floor egg breaks.
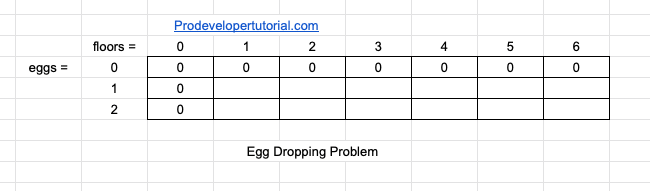
- Initially if you have 0 eggs then the whole row will be 0.
- Similarly, if we have 0 floors, then the min tries will also be 0. Hence we write the column as 0.
It can be updated as below:
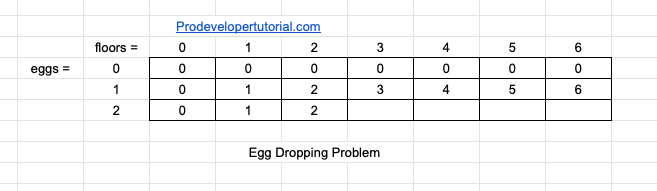
Now you have 1 egg and 6 floors. So you drop the egg from 1st floor, the egg did not break. Again you go to 2nd floor and drop it, egg did not break. Hence you do similar operation from 3rd , 4th, 5th, 6th floor. Hence if you have 1 egg and n floors, the min number of tries will be equal to the floor value.
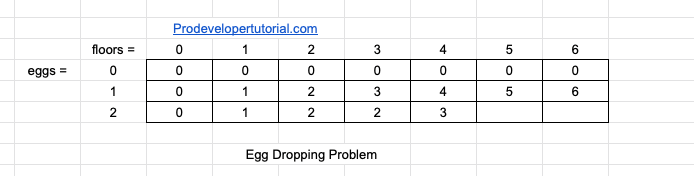
Hence we can update the DP array as below
Now we have 2 eggs.
So again we have 2eggs and 1 floor. SO maximum tries will be 1.
Again we have 2 eggs and 2 floors. So first we try from first floor, we throw the egg and we tried 1 tries.
Now, if the egg breaks, we will be having 1 egg and 1 floor.
else if the egg did not breaks, we will be having 2 egg and 1 floor.
Hence we check the value of DP [1, 1] and DP[2, 1].
Remember our recursive formula:
1 + max [dp[1, 1], dp [2, 1]]
i.e 1 + max[1, 1] = 2
Now concentrate:
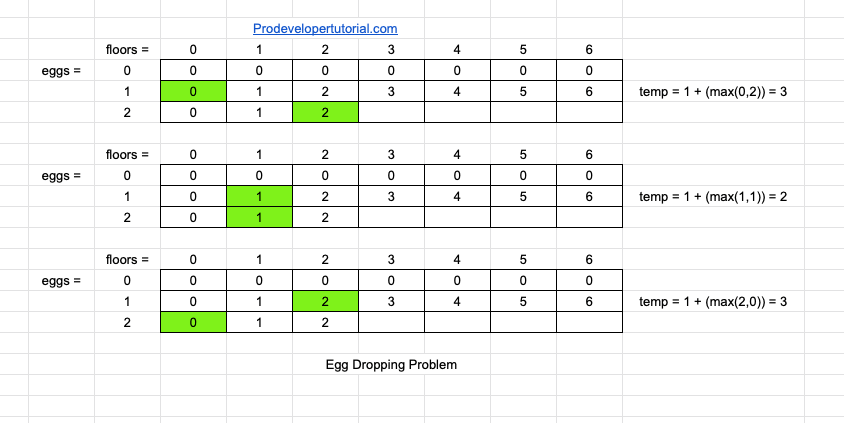
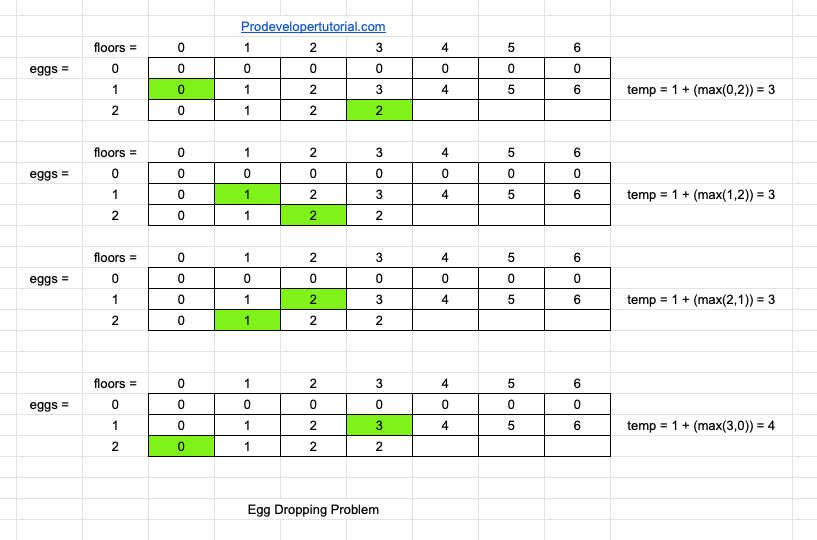
Now we have 2 eggs and 3 floors.
For that, we shall have 2 pointers as shown in image below, and initially we get the max_value +1. Hence from the above got max values, we take the min value and update.
i.e first we compare
1+ max[0, 1] =2
1+ max[1, 1] =2
1+ max[0, 2] =3
Now we have 3 values in the temp i.e [2, 2, 3]. We should take the min of the 3 values. i.e 2
Now we shall solve in similar way when we have 2 egg and 4 floors
Now in the temp array we have 4 values [3, 3, 4, 3]. Min value is 3.
In similar way we calculate where we have 5 floors and 2 eggs and 6 floors and 2 eggs.
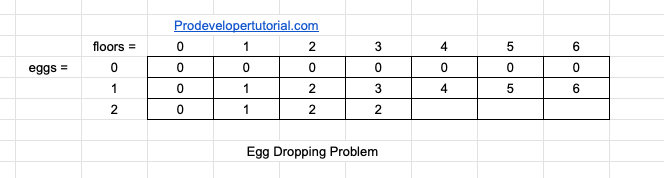
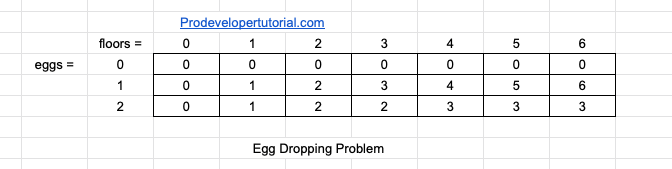
The final DP matrix will be as below:
Hence we need min of 3 tries, when we have 6 floor and 2 eggs.
Solution in C++
#include <iostream>
using namespace std;
// helper function to get max number
int max(int a, int b)
{
return (a > b) ? a : b;
}
int egg_drop_problem(int no_of_eggs, int no_of_floor)
{
// Base case: if no floor or only one floor
// return.
if (no_of_floor == 1 || no_of_floor == 0)
return no_of_floor;
// We need no_of_floor trials for one egg and no_of_floor floors
if (no_of_eggs == 1)
return no_of_floor;
int min = INT_MAX, x, res;
for (x = 1; x <= no_of_floor; x++)
{
res = max(
egg_drop_problem(no_of_eggs - 1, x - 1),
egg_drop_problem(no_of_eggs, no_of_floor - x));
if (res < min)
min = res;
}
return min + 1;
}
int main()
{
int no_of_eggs = 2;
int no_of_floor = 6;
cout << "Minimum number of tries in worst case with "
<< no_of_eggs << " eggs and with " << no_of_floor
<< " floors is "
<< egg_drop_problem(no_of_eggs, no_of_floor) << endl;
return 0;
}
Output:
Minimum number of tries in worst case with 2 eggs and with 6 floors is 3