Dynamic Programming: Building Bridges

In this tutorial we shall solve building bridges problem with help of DP. This is a classical DP problem.

Problem statement:

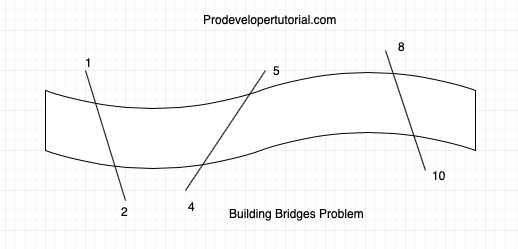
Given a river, you need to build a bridge across the river in such a way that only he pair given can form a bridge, and no bridges should be crossing each other.

Example, given the points [1, 2] [5, 4] [8, 10], the bridges can be formed as below:

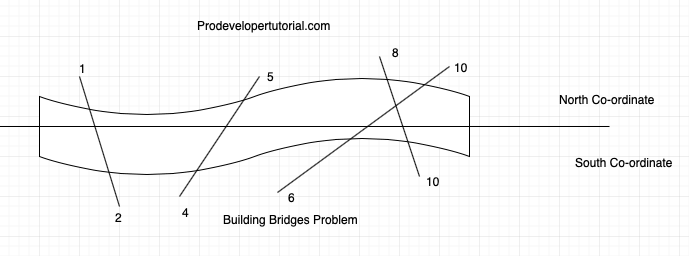
Below bridges are invalid

The above bridges are invalid because the bridge [10, 6] is crossing [8, 10].

The top is north co-ordinate; bottom is south co-ordinate.

Hence according to the given question, you are given pair and you need to build maximum number of bridges by satisfying the above condition.

We are going to solve this problem with the help of DP and longest common subsequence.

This problem can be solved by given steps :

1. Sort the south co-ordinate in ascending order.
2. Find out the longest increasing subsequence for north co-ordinates
3. Join the bridges in Longest Increasing Subsequence.

Example:

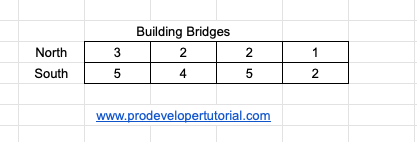
Consider the co-ordinates as below:

Step 1: Sort according to south co-ordinates

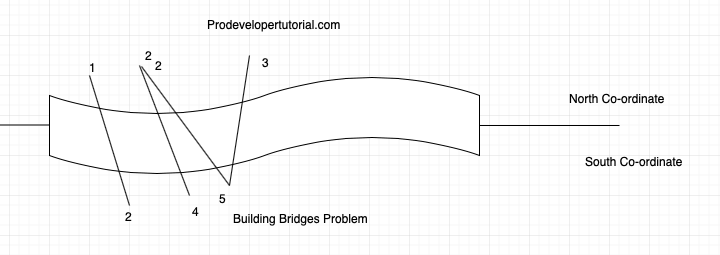
Step 2: Find longest increasing subsequence

Here the sorted order is the longest increasing subsequence.

There is a small change when you compare to original Longest Increasing Subsequence algorithm.

i.e. in original algorithm, we only choose the element if the next element is greater. But here we also choose if the element is equal also.

Solution in C++

#include <iostream> 
  
using namespace std; 
  
// north-south bridge co-ordinates 

struct bridge_co_ordinates
{ 
    int north, south; 
}; 
  
// comparison function to sort bridge co ordinates
bool compare(struct bridge_co_ordinates a, struct bridge_co_ordinates b) 
{ 
    if (a.south == b.south) 
        return a.north < b.north; 
    return a.south < b.south; 
} 
  

int get_max_bridges(struct bridge_co_ordinates values[], int n) 
{ 
    int dp_array[n]; 
    for (int i=0; i<n; i++) 
        dp_array[i] = 1; 
          
    sort(values, values+n, compare); 
      
    // logic of longest increasing subsequence applied on the north coordinates 
    for (int i=1; i<n; i++) 
        for (int j=0; j<i; j++) 
            if (values[i].north >= values[j].north  
                && dp_array[i] < 1 + dp_array[j]) 
                dp_array[i] = 1 + dp_array[j]; 
          
          
    int max = dp_array[0]; 
    for (int i=1; i<n; i++) 
        if (max < dp_array[i]) 
            max = dp_array[i]; 
             
    return max;         
} 
  

int main() 
{ 
    struct bridge_co_ordinates values[] = {{3, 5}, {2, 4}, {2, 5}, {1, 2}}; 
    int n = 4; 
    cout << "Maximum number of bridges = " << get_max_bridges(values, n);     
    return 0; 
}

Output:

Maximum number of bridges = 4

List Of Tutorials available in this website: