In this tutorial we shall solve min edit distance with help of DP.
Problem statement:
You are given 2 strings. You need to find min distance such that the strings are equal.
You will be able to:
- Insert a character
- Delete a character
- Replace a character.
Example 1:
String 1 = ram
String 2 = sam
In the string 2, replace “s” with “r”. Both the strings are equal. Hence min operation is 1.
Example 2:
String 1 = ram
String 2 = sam hi
Min operation will be 3. Because, replace “s” with “r” in string 2 and insert “hi” in string 1. Hence 3.
We shall solve this problem with help of DP.
Consider the 2 strings as given below:
String 1: a b c d e
String 2: a x d y
By looking at the strings we need 3 operations.
i.e
Operation 1: Convert x to b in string 2
Operation 2: Delete c in string 1
Operation 3: Convert y to e in string 2
As usual we form a dp table to hold number of operations needed. At the end we will get total number of operations.
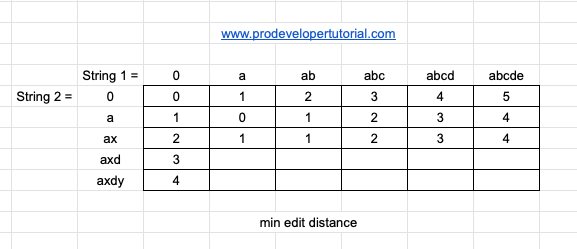
Initially our DP table will be as below:
In the row we have combination of string 1 starting form 0. In the column we have combinations of string 2 starting from 0. As informed earlier, it is always good to start DP from 0.
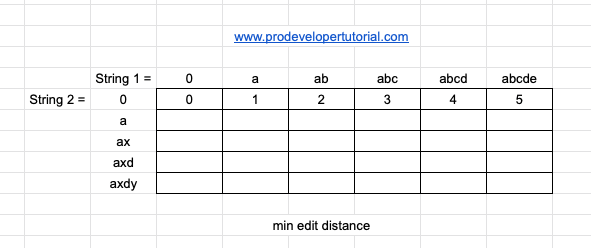
For row 0, it means, we don’t have any characters. Hence [0, 0] will be 0.
Now [0, a] to make no string to “a” it will take 1 operation.
Now [0, ab] to make no string to “a” it will take 2 operations.
Now [0, abc] to make no string to “a” it will take 3 operations.
Now [0, abcd] to make no string to “a” it will take 4 operations.
Now [0, abcde] to make no string to “a” it will take 5 operations.
Hence the final DP table will be as below:
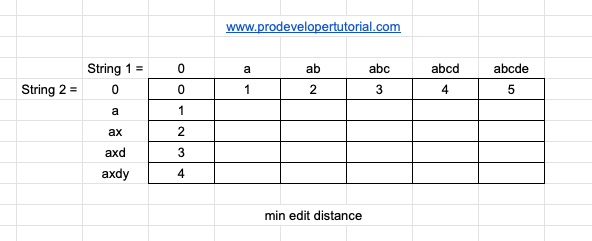
Similarly, for the column ‘0’ we fill the DP table as below
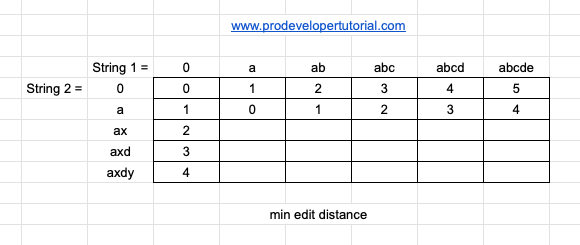
Now to the 2nd row “a”.
Now [a, a] to make “a” string to “a” it will take 0 operation.
Now [a, ab] to make “a” string to “ab” it will take 1 operation.
Now [a, abc] to make “a” string to “abc” it will take 2 operations.
Now [a, abcd] to make “a” string to “abcd” it will take 3 operations.
Now [a, abcde] to make “a” string to “abcde” it will take 4 operations.
Now we shall do the same operation to row 3 i.e “ax”
Now [ax, a] to make “a” string to “a” it will take 1 operation.
Now [ax, ab] to make “a” string to “ab” it will take 1 operation.
Now [ax, abc] to make “a” string to “abc” it will take 2 operations.
Now [ax, abcd] to make “a” string to “abcd” it will take 3 operations.
Now [ax, abcde] to make “a” string to “abcde” it will take 4 operations.
So by looking at above pattern, can we arrive at a DP formula?
Yes, we can arrive as below:
When ever you arrive at a cell, you need to take min of element at it’s left, element at it’s top, element at it’s diagonal and add 1 to it. If the last element is different.
If the last element is same, then calculate the min of the element to it’s left and diagonal.
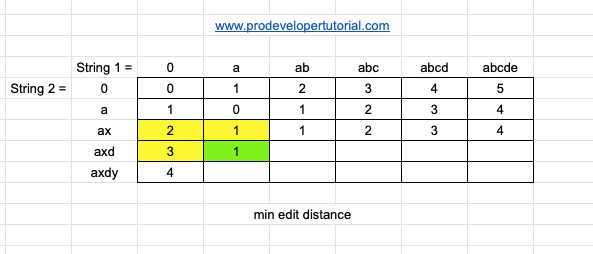
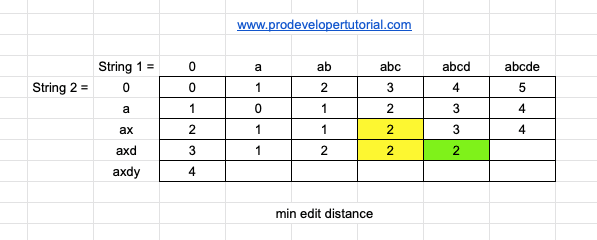
Now we shall take 4th row i.e “axd”
Now [axd, a] as the last element “x” and “a” are different, take the min of 3 elements and add 1.
min[3, 2, 1] + 1 = 2
Now [axd, ab] as the last element “d” and “b” are different, take the min of 3 elements and add 1.
min[1, 1, 1] + 1 = 2
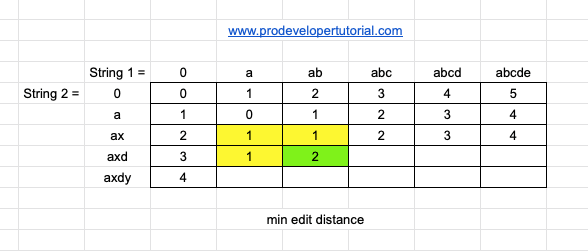
Now [axd, abc] as the last element “d” and “c” are different, take the min of 3 elements and add 1.
min[2, 1, 2] + 1 = 2
Now [axd, abcd] as the last element “d” and “d” are same, take the min of element to it’s left and diagonal.
min[2, 2] = 2
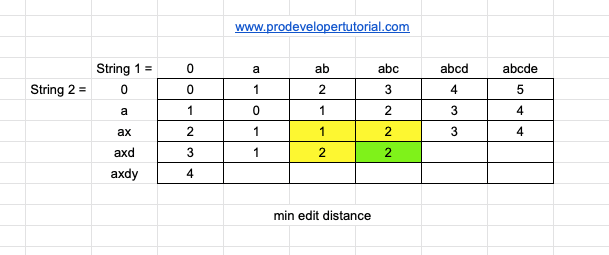
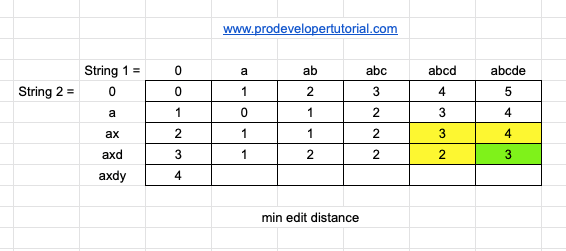
Now [axd, abcde] as the last element “d” and “e” are different, take the min of 3 elements and add 1.
min[2, 3, 4] + 1 = 3
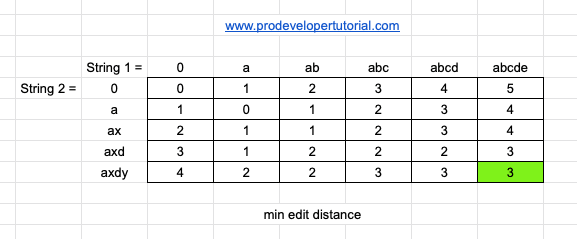
Similarly, we calculate the same way for rest of the array. The final result will be as below:
From the image, we can see that we need 3 operations.
Solution in C++
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int min_distance(string word1, string word2)
{
int m = word1.size();
int n = word2.size();
vector<vector<int> > dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++)
{
dp[i][0] = i;
}
for (int j = 1; j <= n; j++)
{
dp[0][j] = j;
}
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (word1[i - 1] == word2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1];
} else
{
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i][j - 1], dp[i - 1][j])) + 1;
}
}
}
return dp[m][n];
}
int main()
{
string str1 = "abcde";
string str2 = "axdy";
cout << "Minimum edit distance is " << min_distance(str1, str2)<<endl;
return 0;
}
Output:
Minimum edit distance is 3