In the previous chapter we learnt on conceptual level on creating a segment tree. In this chapter we shall learn on actually how to implement and search for range queries.
The topics we are going to discuss are as below:
- Partial Overlap
- Total Overlap
- No – Overlap
- Construct Segment Tree
In the first section we shall learn the different methods to perform range queries. In the next section we shall see how to construct a segment tree.
-
Performing range queries.
While performing range queries, you are given a search range, you need to check with the range in hand. We shall call range in hand as Parent range.
Point to be noted here is, the range query is performed with respect to the search query range. What is that? We shall see further.
To perform range queries we have 3 different methods to do it.
- Partial overlap
- Total Overlap
- No-overlap
Now we shall try to understand the above 3 methods by taking simple examples.
-
Partial Overlap
Consider the parent range is “0-6” and we need to find min in the range of “3-4”. Here we can say that the query is a partial overlap for the parent range. It doesn’t matter if the parent range “0-6” in total overlap for search range “3-4”.
Below image will explain in detail:
Here the search range should overlap the parent. We look overlap with respect to search query. When we have partial overlap, we look at both left and right child.
-
Total Overlap
Consider the parent range is “0-2” and the search query of range “0-3”. Here we can say that the query is total overlap of the parent range.
As you can see in the above image, the query range totally overlap the parent range.
In case of total overlap, we will return the value as the result.
-
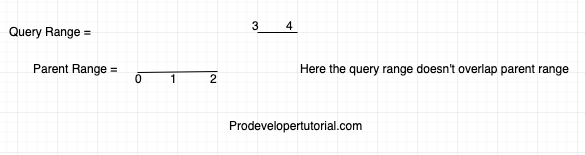
No Overlap
Consider the parent range “0-2” and query range “3-4”, there is no overlap. In this case we return Int_Max stating that there is no overlap of search query with parent query.
Now that we have a brief idea of the 3 rules, we shall take an example and understand them better.
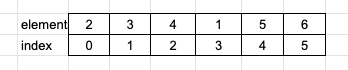
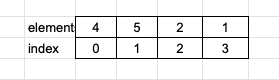
Consider the array as below:
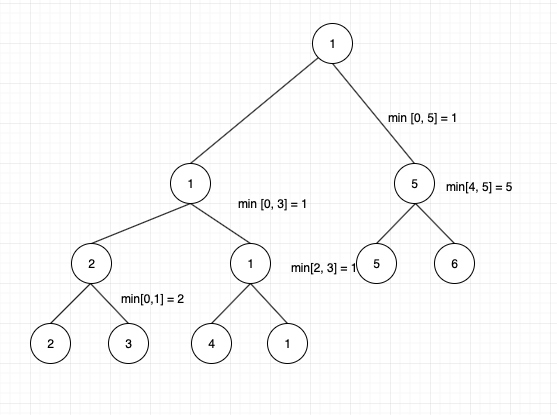
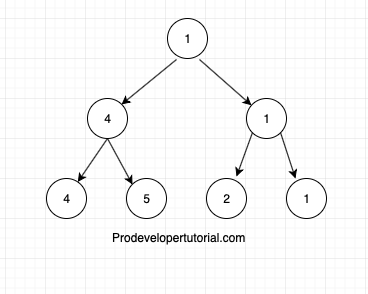
And min query segment tree as below
Now we need to find the min of “3-5”.
At first “3-5” is a partial overlap of “0-5”. Hence we need to check both left and right children.
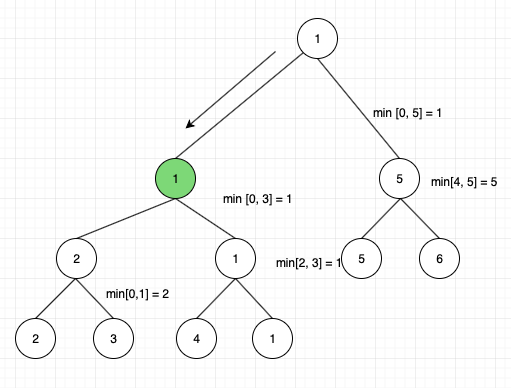
First we shall go to left child.
Here the node with min query index of [0, 3] is a partial overlap for the search query [3, 5]. Hence we again check for left and right children for that node.
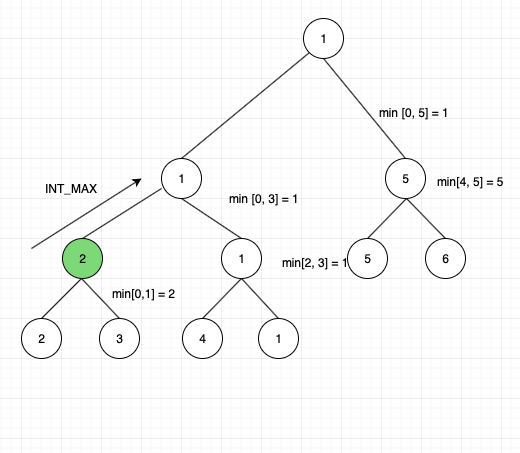
Again we take left child with min query index of [0, 1]. As [0, 1] is no-overlap for the query range of [3, 5] we return INT_MAX.
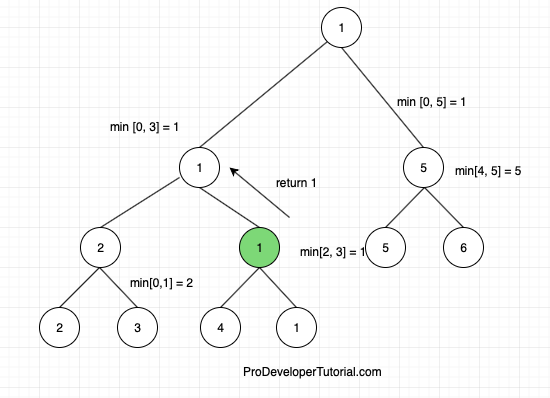
Now we shall go to right child for the node [0, 3]. The right child is [2, 3], as it is a partial overlap return 1.
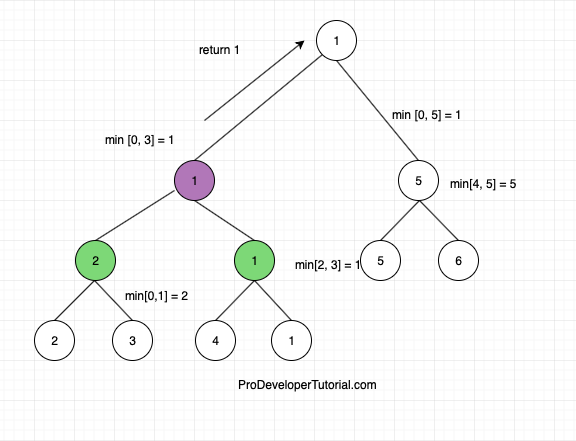
Now at the parent node of query [0, 3], we have to choose the min of both left and right child. i.e min(INT_MAX, 1). Return 1.
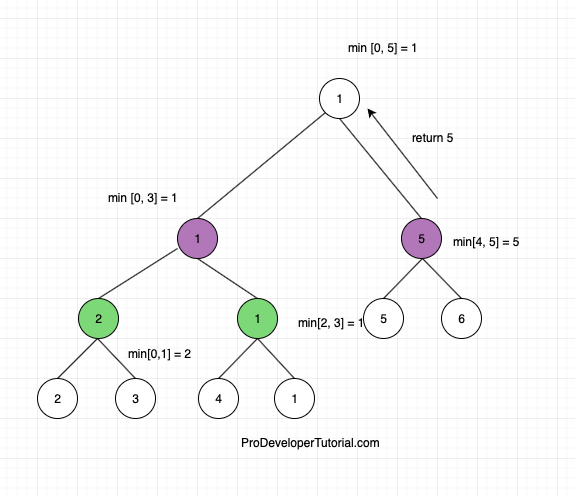
Now we check the right child of the parent node with query [0, 5]. The right child is [4, 5]. This is a partial overlap for our search query [3, 5]. Hence return 5.
At the parent node of query [0, 5], choose the min of left child and right child. i.e min [1, 5] is 1.
Hence the min element in the range [3, 5] is 1.
How to build a segment tree?
In the previous section we saw to how query in a segment tree. In this section we shall see how to build a segment tree.
A segment tree at it’s basic, is an array. We calculate the min value and place them at appropriate index. Let us understand with help of an example.
Consider the array as below:
The segment tree will be:
So from above image, for 4 elements we need 7 spaces.
Hence the total number of spaces needed for segment tree, given an array is
Size_of_array * 2 – 1.
In our example, the size of array is 4. Hence the total size required for segment tree is “4 * 2 -1 = 7”.
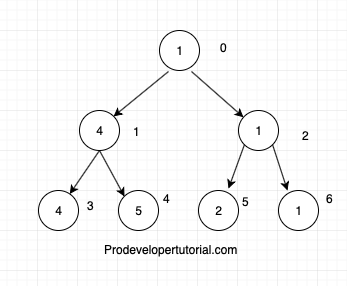
Below is the tree with index.
Segment tree array:
Now for any parent, to get to left child use “ 2 * i + 1”
Now for any parent, to get to right child use “ 2 * i + 2”
To get to the parent use “( i – 1 )/2”
Implementation of Min Range Query Segment Tree in Cpp
#include <iostream>
using namespace std;
void build_min_tree(int arr[], int* tree_min, int start, int end, int ind)
{
if(start == end)
{
tree_min[ind]=arr[start];
return;
}
int mid = (start+end)/2;
build_min_tree(arr, tree_min, start, mid, 2*ind);
build_min_tree(arr,tree_min, mid+1, end, 2*ind+1);
tree_min[ind] = min(tree_min[2*ind],tree_min[2*ind+1]);
}
int min_in_range(int l, int r, int index, int start, int end ,int* tree_min)
{
if(end<l || start>r) return INT_MAX; //no overlap case
if(l<=start && r>=end) return tree_min[index]; //total overlap case
int mid = (start+end)/2;
return min(min_in_range(l, r, 2*index, start, mid, tree_min), min_in_range(l, r, 2*index+1, mid+1, end, tree_min));
}
int main()
{
int n;
cout<<"Enter number of elements \n";
cin >> n;
int arr[n];
cout<<"Enter "<<n <<"elements\n";
for (int i = 0; i < n; ++i)
{
cin >> arr[i];
}
int tree_min[4*n];
build_min_tree(arr, tree_min, 0, n-1, 1);
int l;
int r;
cout << "Enter lower range and higher range to perform min range query:" << endl;
cin >> l >> r;
cout << "Minimum Number in range : " << min_in_range(l,r,1,0,n-1,tree_min) << endl;
return 0;
}
Output:
Enter number of elements 5 Enter 5elements 1 2 3 4 5 Enter lower range and higher range to perform min range query: 0 3 Minimum Number in range : 1
Further Reading: