Segment tree is a special tree that is based on ranges. In this chapter we shall learn about basics of segment tree. In the next chapter we shall learn about the implementation and also about Lazy Propagation.
Need for Segment Tree:
Usually segment trees are used to find solution to the problems based on the range query in the array.
Below are the 2 basic uses cases of range queries.
- Find the sum of given range in an array.
- Find the min value in the given range in an array.
We shall learn in-depth of both of the types, by seeing the generic solution and also with segment tree solution.
-
Finding the sum for given range in an array.
Consider the array below
In the above array, there are 9 elements and you are asked to find the sum of elements from index 2 to 5.
This can be done by running the loop from index 2 to 5.
i.e 5 + 1 + 2 + 3 = 11
But if you are asked to find the sum from index 0 to 8, this will be the worst case. You will need to run the loop for all the elements. Hence it will take O(n) time.
Is there a way to get the solution efficiently?
Yes, we can do it with help of segment tree.
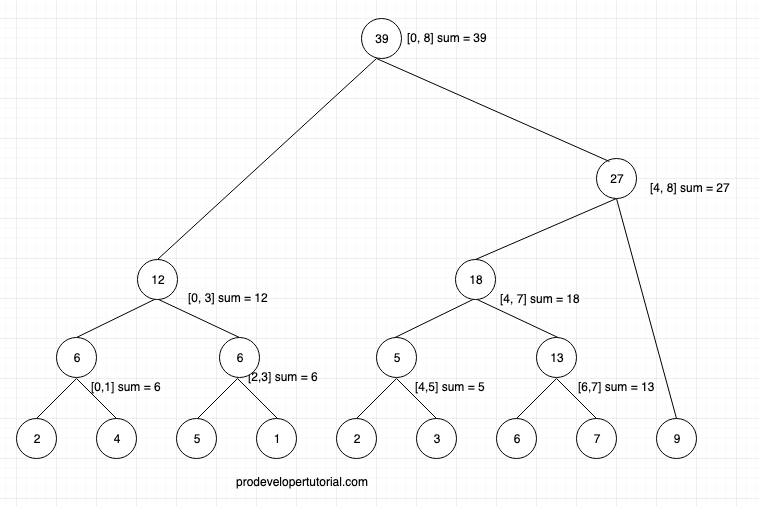
We shall see how to build a segment tree for the array elements above.
At the minimum, a segment tree can be constructed by keeping all the elements of the array as leaf node and then constructing from bottom to top.
In the series of steps below, we shall see how we can construct segment tree for sum range query.
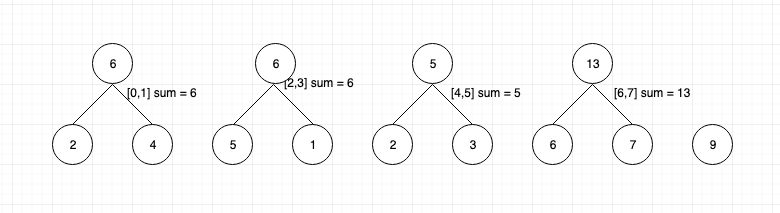
First consider all the nodes as root node.
Now we shall make the sum of the range [0, 1] [2, 3] [4, 5] [6, 7] [8]
It can be represented as below:
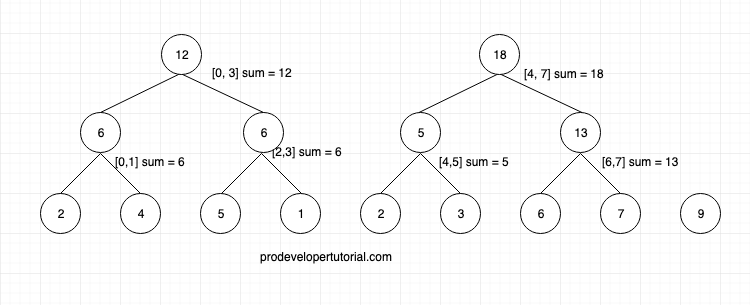
Now, we shall calculate the sum for the range [0, 3] [4, 7] [8].
As we have already have calculated sum for sub range, it’s just matter of adding those sub ranges.
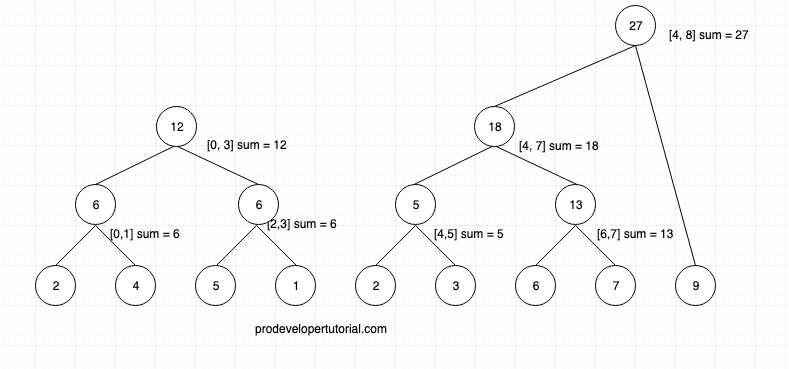
Now we shall calculate the range for [4, 8].
Now finally calculate the range for [0, 8].
This is how we build segment tree for sum range query. Now if you were to get the sum of range [0, 3], then you can directly get the sum = 12. This can be done for O(logn) time at worst case.
-
Find the min value in the given range in an array,
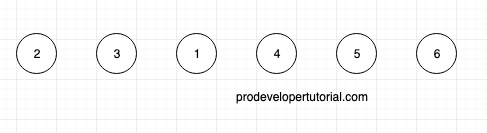
Consider the below array
You are asked to find the minimum element from the range 3 to 6. The answer will be 1. But if you are to find the min element in the whole array, and the min element is at the end of the array, it will take O(n) time at worst case.
This can be improved to O(logn) time if we use segment tree.
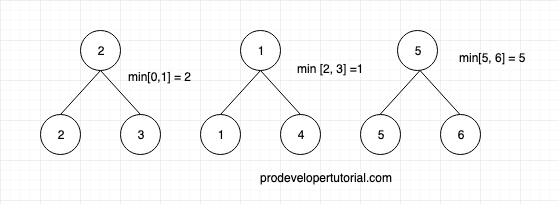
Similar to previous section, make all the elements of the array as leaf node. As shown below.
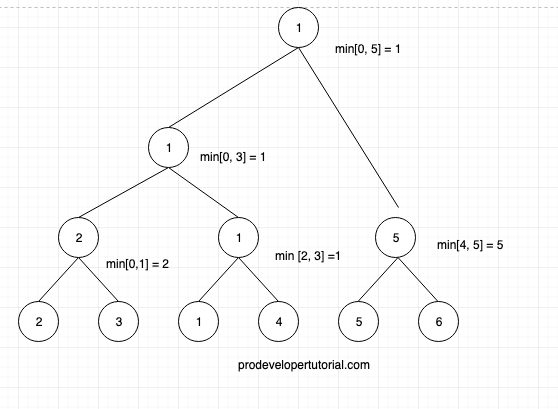
Now we shall find the shortest value for the range [0, 1] [2, 3] [4, 5] as shown below:
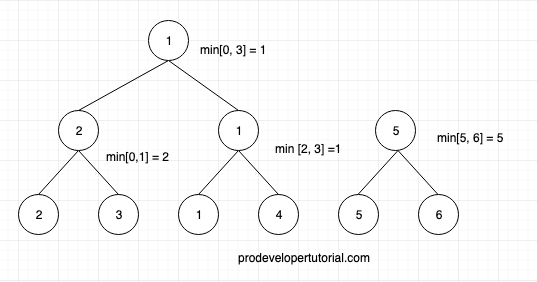
Now we shall find the shortest value for the range [0, 3].
Now we shall find the shortest range for whole array [0, 5]. Thus completing the segment tree for shortest value in the range.
That’s all for this chapter. In the next chapter we shall know in depth on creating segment tree and the steps involved in querying for range values.
Further Reading: