In this chapter you are going to learn about below topics:
1.1 What is a tree data structure?
1.2 Types of trees
1.3 Types of tree traversal
1.4 What is a tree?
1.5 How a tree is represented?
1.6 Full tree representation.
1.7 Different Terminology involved in Trees.
1.8 Applications of Tree.
1.9 Properties of Tree.
1.1 What is a tree data structure?
Trees are non linear data structures. They are used to represent hierarchical relationships.
It is a very interesting data structure. Data Structure like array, Linked List, Stack, Queue is linear data structure. They have a logical start and logical end.
1.2 Types of trees:
1. Binary search tree
2. Heaps
3. Expression Trees
4. Ordered Trees
5. Red-black trees
6. Decision Trees
1.3 Types of tree traversal
1. Pre-Order traversal
2. In-Order traversal
3. Post-Order traversal
1.4 What is a tree?
1. A tree is a collection of nodes and edges.
2. Every tree will have a special node called as “root node”, that will be the entry point for that tree.
3. The nodes will be connected together with edges or path.
4. There will always be only one path from root node to any other node in a tree.
1.5 How a tree is represented?
As we know that a tree is a collection of nodes and edges.
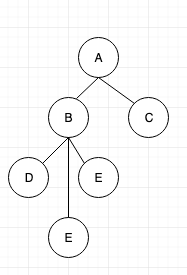
Nodes are usually represented as circular in shape. But they can also be represented in different shape as shown below:
Edge or a path is represented by a straight line. As in tree, you can traverse from top to bottom, there is no need to use arrow lines.
1.6 Full tree representation:
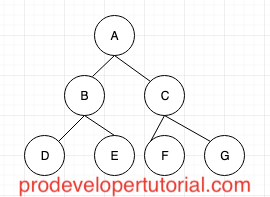
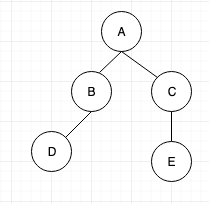
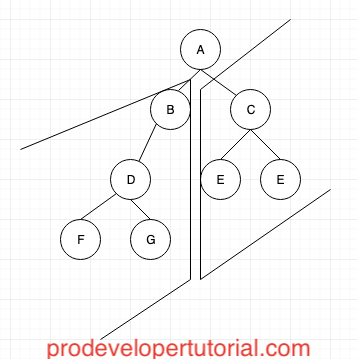
From the above image we can see that:
“A” is the root node.
“D” “E” “F” “G” are the leaf nodes. A leaf node is a node that doesn’t have any child.
“B” “C” are internal nodes.
1.7 Different Terminology involved in Trees.
1. Parent Node
A node directly above a given node is called as a parent node.
Note: A root node will not have any parent node.
In the above image, A is the parent for both “B” and “C” nodes.
B is the parent node for “D”.
2. Child Node:
A node, that is directly below a node, is called as child node.
From the image above,
“D” and “E” are children of “B”
“B” and “C” are children of “A”
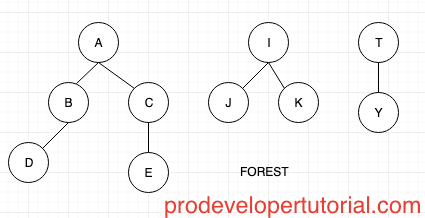
3. Siblings:
All the nodes or children which have a common parent are collectively known as siblings.
From the image above,
“D” “E” “F” are siblings, as they share common parent “B”.
4. Forest:
Set of independent trees are called as forest.
5. Leaf node:
A node with no child is called as leaf node.
Here “D” “E” are leaf node.
6. Internal Nodes:
The nodes with at least one child can be called as internal nodes.
7. Ancestor and descendants:
If there is a path from “A” to “B” then “A” can be called as ancestor of “B”. “B” is called as descendant of “A”.
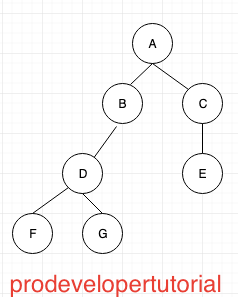
From the image above, “A”, “B”, “D” are ancestors for “G”. And “G” is the descendant for all the above nodes.
1.8 Applications of Tree:
1. Index of a book can be considered as a tree. A book is organized into several chapters, each chapter is divided into sections and sub sections.
2. File system in Unix or Linux. The file system will start from a root, then it will branch out according to requirement.
1.9 Properties of Tree:
1. A tree can have sub tree
2. A tree with “n” nodes will be having exactly “n-1” edges.
Depth of a node:
The depth of a node is the length of the path from root to that node.
i.e the number of edges from root to that node.
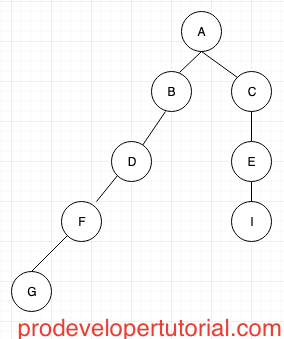
From the image above,
Depth of node “G” is 4
Depth of node “I” is 3
Height of a node:
Height of a node is the longest path from that node to a leaf node.
From the image above,
The height of node “D” is 2. Because D -> F -> G
Height of a Tree:
The height of a tree is defined as the height of root node.
Hence from the above image, the height of the tree is 4. Because A -> B -> D -> F -> G
Further Reading: