In this chapter we shall learn about:
2.1. Introduction to binary tree
2.2. Examples of binary tree
2.3. Strict binary tree
2.4. Complete Binary Tree
2.5. Level of binary tree
2.6. Perfect Binary Tree
2.1 Introduction to Binary Tree
A binary tree is a special kind of tree that can have at-most 2 children.
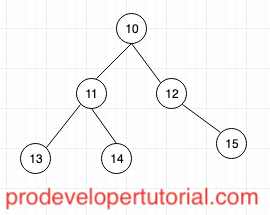
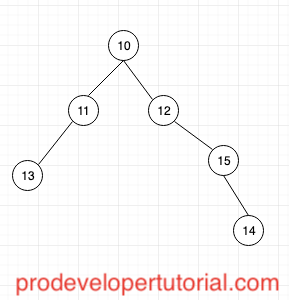
2.2 Some of the example is shown below:
As a node can have a maximum of 2 children, the child to the left is called as left child and to the right is called as right child.
A node can have both left and right children or only left or right child.
A node with no child is called as leaf node.
2.3 Strict or Proper binary tree
If each node has either 2 or 0 children is called as strict binary tree.
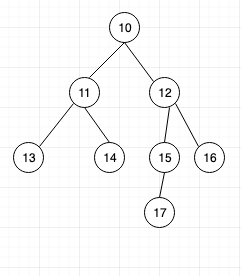
2.4 Complete Binary Tree
A binary tree is called as complete binary tree if all the level except the last level are completely full and the last level has all its nodes to its left.
Example
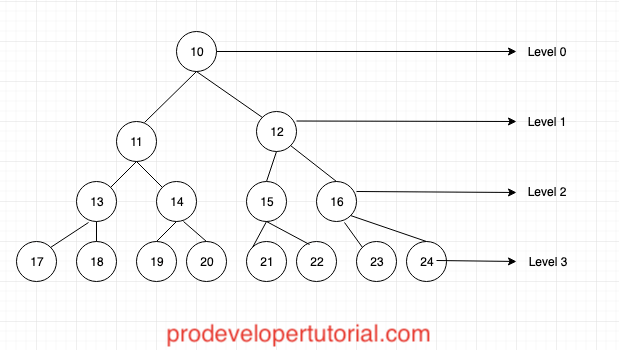
2.5 Level of binary tree
The nodes at same depth can be called as nodes at the same level.
Root node in a tree will have level 0.
Hence from the image above, we can infer that the maximum number of nodes at a particular level is 2^i. Where “i” is the level.
At level 0, 2^0 = 1
At level 1, 2^1 = 2 at max 2 nodes
At level 2, 2^2 = 4 at max 4 nodes
At level 3, 2^3 = 8 at max 8 nodes
2.6 Perfect Binary Tree:
If the all the levels are completely filled, such a tree is called as perfect binary tree.
Hence the total number of nodes in a perfect binary tree will be 2^(num of level) -1;
Hence the total number of nodes for a level 4 perfect binary tree will have 2^4 -1 = 15 nodes.
Further Reading: