Minimum Cost Path in CPP

You are given a m x n matrix with elements which represents cost. your goal is to start from top left and reach to bottom right with minimum cost. You can move only down or right.

Example:

Input:
[
  [1,3,1],
  [5,7,1],
  [3,8,1]
]

Output: 7
Minimum cost path is = 1 -> 3 -> 1 -> 1 -> 1

This problem can be solved with the help of Dynamic Programming.

We take a new (m * n) array. Then we shave the values by computing using a formula [given at the end of the explination].

Let us understand the problem with the help of an example.

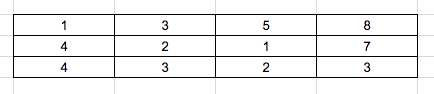
Consider the below array:

Here we need to find the minimum sum/cost from the top right corner to bottom left corner. We can only move to the right or move bottom.

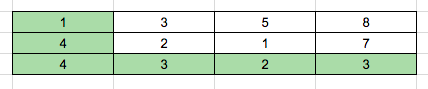
Consider that we want to find the path for the highlighted image below:

The total cost will be “1 + 4 + 4 + 3 + 2 + 3 = 17”.

But we need to find the min cost.

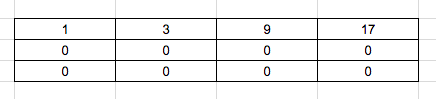
We shall solve by taking another array to calculate and store the values. Initialize arr[0][0] to 1, because it is the first path and can only be reached by cost 1.

Now we shall solve the first row.

To reach arr[0][1]  there is only 1 way, from arr[0][0]. Hence the total cost will be “1 + 3 = 4”.
To reach arr[0][2]  there is only 1 way, from arr[0][1]. Hence the total cost will be “1 + 3 + 5 = 9”.
To reach arr[0][3]  there is only 1 way, from arr[0][2]. Hence the total cost will be “9 + 8 = 17”.

Now we solve 1^st column

To reach arr[1][0]  there is only 1 way, from arr[0][0]. Hence the total cost will be “1 + 4  = 5”.
To reach arr[2][0]  there is only 1 way, from arr[0][1]. Hence the total cost will be “5 + 4  = 9”.

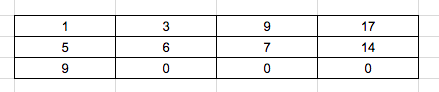
Now coming to 1^st row:

To reach arr[1][1]  there is only 2 ways, from arr[0][1] or arr[1][0]. But we need to take the minimum path. Hence we take the min cost of both the ways. i.e min(5, 4). The min cost is 4, we add it with present cost. Hence the total cost is 6.

To reach arr[1][2]  there is only 2 ways, from arr[0][2] or arr[1][1]. But we need to take the minimum path. Hence we take the min cost of both the ways. i.e min(6, 9). The min cost is 6, we add it with present cost. Hence the total cost is 7.

Similarly arr[1][3] will be 14.

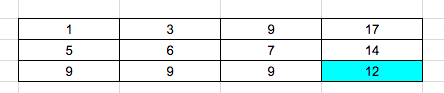
After solving the last row, the result is highlighted as shown below:

12 is the final result.

Hence from the above analysis, we can come to a conclusion:

The cost of arr[i][j] = arr[i][j] + min(arr[i - 1][j], arr[i][j - 1]);

Solution in C++

#include<iostream>
#include<vector>

using namespace std;



int get_min_path(vector<vector<int>>& input) 
{
	//get the row size
	int m = input.size();

    //get the column size
	int n = input[0].size(); 

	//Create a 2D array and initialize it with 1
	vector<vector<int> > result(m, vector<int>(n, input[0][0]));

//Solve first row
	for (int i = 1; i < m; i++)
		result[i][0] = result[i - 1][0] + input[i][0];

//Solve first column
	for (int j = 1; j < n; j++)
		result[0][j] = result[0][j - 1] + input[0][j];

	for (int i = 1; i < m; i++)
		for (int j = 1; j < n; j++)
			result[i][j]  = min(result[i - 1][j], result[i][j - 1]) + input[i][j];

		return result[m - 1][n - 1];
	}

int main()
{
	//Declare 2D vector
	int row = 3;
	int column = 4;
	vector<vector<int> > input = { { 1, 3, 5, 8 },
                                   { 4, 2, 1, 7 },
                                   { 4, 3, 2, 3 },
                                  };

    cout<< "The input array is "<<endl;

    for (int i = 0; i < input.size(); i++)
    {
    	for (int j = 0; j < input[0].size(); j++)
    	{
    		cout<< input[i][j]<<" ";
    	}
    	cout<<endl;
    }

    cout<< "\nThe min path is =  "<<get_min_path(input)<<endl;

	return 0;
}

Output:

1 3 5 8
4 2 1 7
4 3 2 3



The min path is =  12

Please comment below with your solutions.

List Of Tutorials available in this website: