Problem Explanation:
A bike is located at the top-left corner of a m x n matrix.
Bike can only move either down or right at any point in time. Bike is trying to reach the bottom-right corner of the matrix.
There are some obstacles along the way, find the number of ways that bike can reach the end avoiding the obstacles.
Example 1: Input: [ [0,0,0], [0,1,0], [0,0,0] ] Output: 2
Before solving this solution, we have previously solved similar problem called “Unique Paths”.
Similar to the above problem, this problem can also be solved with the help of Dynamic Programming.
We understand the solution by taking an example below:
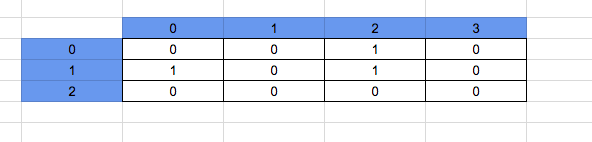
Consider the below 3 x 4 matrix as shown in image below:
We solve by taking one grid at a time.
So the number of ways to arr[0][0] is 1.
The number of ways to arr[0][1] is 1, because we can arrive at this point by left side.
The number of ways to arr[0][2] is 0, because there is an obstacle.
The number of ways to arr[0][3] is also 0, because there is an obstacle at arr[0][2].
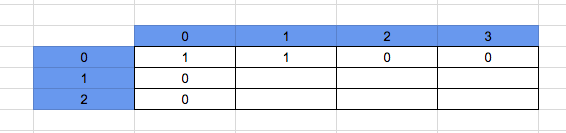
So the matrix will look as below:
The number of ways to arr[1][0] is 0, because there is an obstacle.
The number of ways to arr[1][1] is 1, because there is a way from arr[0][1].
The number of ways to arr[1][2] is 0, because there is an obstacle.
The number of ways to arr[1][3] is 0, because there is an obstacle at arr[1][2].
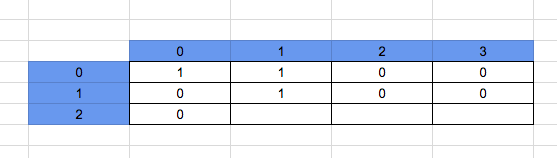
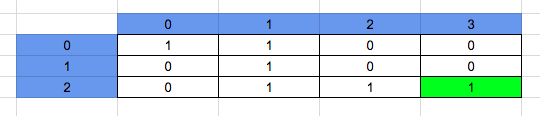
Similarly, we solve the rest of the array, at the end we get the number of ways we can reach the end with the obstacle.
So form the above analysis we can conclude with the formula:
The number of paths at arr[i][j] = arr [i – 1][j] + arr [i][j – 1] if input_array[i][j] != 1 and 0 otherwise.
Solution in C++
#include<iostream>
#include<vector>
using namespace std;
#define m 3
#define n 4
int get_unique_paths_with_obstacle(int arr[m][n])
{
int path [m] [n];
// Base condition
// initialize the array to 0
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
path[i][j]=0;
}
}
// Base condition
if(arr[0][0] == 1) return 0; //no paths if the starting place is itself an obstacle
path[0][0] = 1; //initializing the first position
// set the first row
for(int i=1;i<m;i++)
{
if(arr[i][0]==0)
{
path[i][0] = path[i-1][0];
}
}
// set the first column
for(int i=1;i<n;i++)
{
if(arr[0][i]==0)
{
path[0][i] = path[0][i-1];
}
}
// apply the formula path[i][j] = path [i - 1][j] + path [i][j - 1] if input_array[i][j] != 1 and 0 otherwise.
for (int i = 1; i < m; i++)
for (int j = 1; j < n; j++)
if (!arr[i][j])
path[i][j] = path[i - 1][j] + path[i][j - 1];
return path[m - 1][n - 1];
}
int main()
{
int arr [m][n];
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
// inserting obstacle
if ( (i == 0 && j == 2) || (i == 1 && j == 0)||(i == 1 && j == 2))
{
arr[i] [j] = 1;
continue;
}
arr[i] [j] = 0;
}
}
cout<<"Input array is "<<endl;
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
cout<< arr[i][j]<<" ";
}
cout<<endl;
}
int result = get_unique_paths_with_obstacle(arr);
cout<<"The number of unique paths for a "<<m <<" x "<< n<<" matrix is = "<< result<<endl;
return 0;
}
Output:
Input array is 0 0 1 0 1 0 1 0 0 0 0 0 The number of unique paths for a 3 x 4 matrix is = 1