In this tutorial we shall learn about bipartite graph.
Definition:
A graph G(V, E) is called as bipartite graph if all the vertices (V) can be divided into 2 distinct disjoint non empty sets V1 and V2 such that every edge in the graph connects a vertex in V1 and vertex in V2, so that no edge in graph connects 2 vertices in the same set.
Let us understand the above definition with help of example.
Consider a simple graph below:
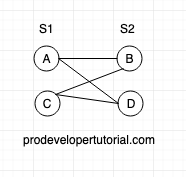
By seeing above graph, we can divide all the vertices into 2 sets as:
S1 = {A, C}
S2 = {B, D}
and it can be written as:
As you can see that there are 2 distinct non-empty sets and no 2 vertices of the same set are connected.
Here you can see that each vertex from one set is connected by every other vertex in other set.
Example 2:
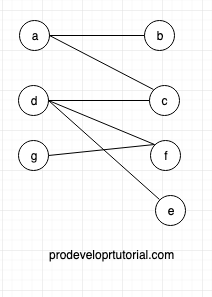
Consider the image below
The above graph, we can divide al the vertices into 2 sets as:
S1 = {A, D, G}
S2 = {B, C, F, E}
Complete Bipartite Graph:
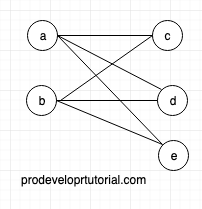
A graph is called complete complete bipartite graph if all the vertices from set 1 are connected to all other vertices of from set 2.
Consider the example below:
As above both vertex “a” and vertex “b” from SET 1 are connected to all other vertices of SET 2.
Further Reading: