In previous chapter we learnt about graph traversal in general. In this chapter we shall learn how to do graph traversal using Stack and Queue.
DFS graph traversal using Stack:
As in DFS traversal we take a node and go in depth, till we find that there is no further path. Then we backtrack to each visited nodes and check if it has any unvisited adjacent nodes. By doing so, we tend to follow DFS traversal.
So to backtrack, we take the help of stack data structure. As you know in stack is based on last in first out, it will help us to backtrack one node by another.
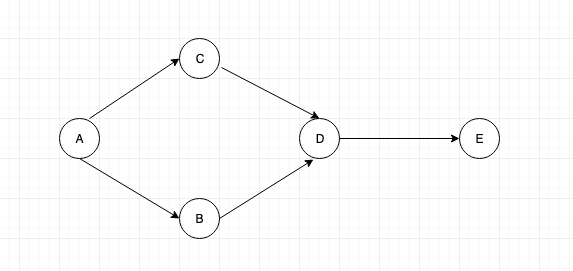
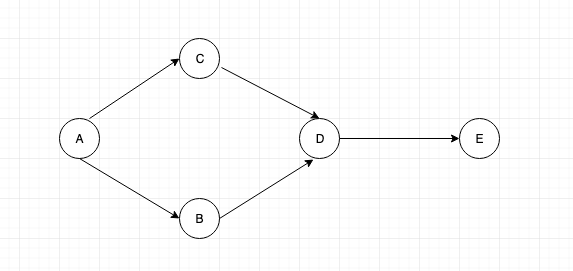
Let us take an example of the graph below:
For this to work, we shall have a stack and another array to maintain the nodes that have been visited.
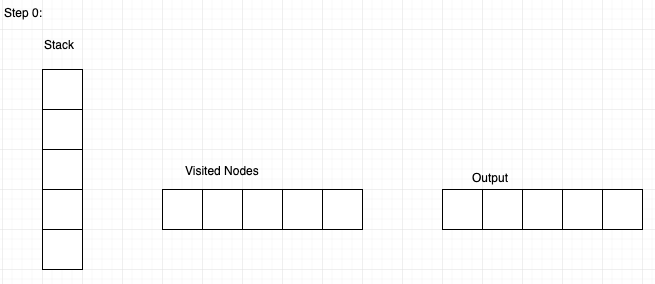
Initially the stack and visited array will be empty.
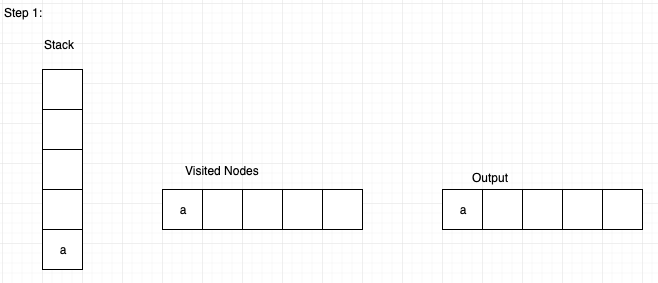
Step 1: Let us visit node ‘a’ and insert it into the stack and mark that node as visited. And print it in output.
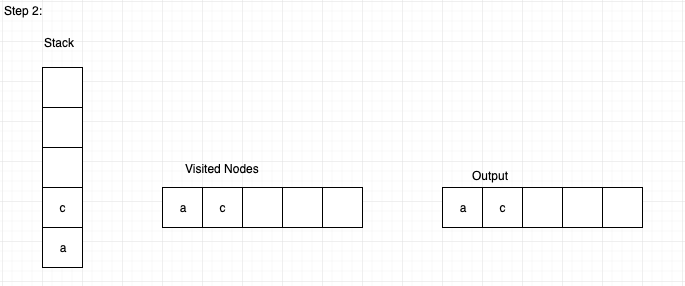
Step 2: Let us visit node ‘c’ and insert it into the stack and mark that node as visited, and print it in output.
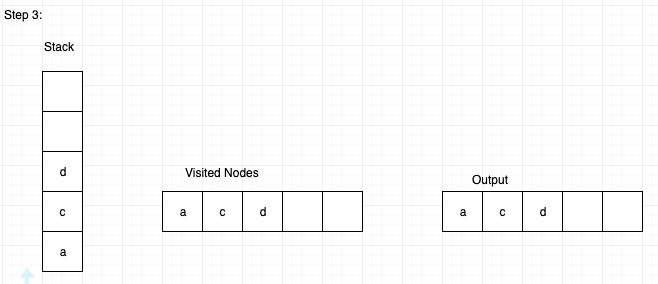
Step 3: Let us visit node ‘d’ and insert it into the stack and mark that node as visited, and print it in output.
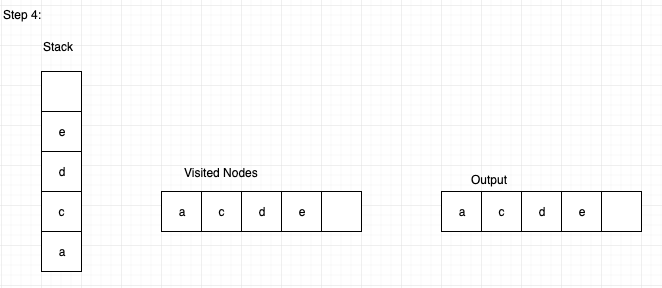
Step 4: Let us visit node ‘e’ and insert it into the stack and mark that node as visited, and print it in output.
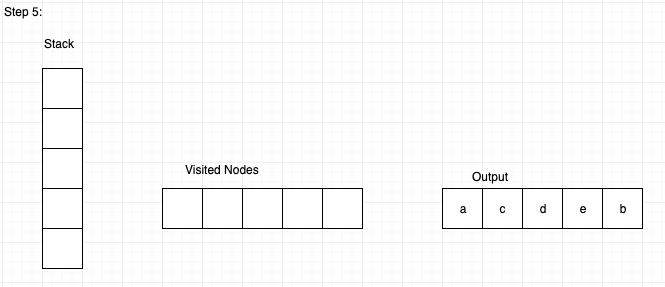
Step 5: Now we see that node ‘e’ is not having any further nodes to explore, hence with the help of the stack, we backtrack.
We pop node ‘e’.
Then we pop node ‘d’, then check if there are any adjacent nodes to it, as the graph is directed, it don’t have any adjacent nodes.
Now pop node ‘c’, and check if it has any adjacent unvisited node. It don’t have any
Now pop node ‘a’ and check if it has any adjacent unvisited node. It has node ‘b’ as unvisited node. Visit it and write it in output.
Then the output will be
A C D E B
BFS graph traversal using Queue:
In BFS traversal we do level by level. Hence we use queue data structure to achieve this. Below are the steps for BFS traversal using queue.
Let us consider the same graph as above.
In BFS also, we need a queue and an array to hold the visited elements. Initially both will be empty.
Step 1: we visit node ‘a’ then go to its adjacent nodes and write it in queue and mark them as visited.
As there are no further adjacent nodes for ‘a’, pop from the queue and write it in output.
Step 2:
Now visit node ‘c’ and check if it has adjacent nodes. It has node ‘d’ as its adjacent node. Write it in queue and make it as visited. As there is no other adjacent nodes, pop node ‘c’ from queue and write in output.
Step 3:
Now visit node ‘b’, check if it has any adjacent node. It has node ‘d’, but it is already visited. Hence pop from queue and write in O/P
Step 4:
Now visit node ‘d’. Check it has any adjacent node that is not visited. It has node ‘e’, insert in queue and mark it as visited. Pop ‘d’ from queue.
Since all the nodes has been visited, pop e from queue. Hence we get the solution as below:
Note:
DFS:
We us stack to backtrack when we hit a dead end, while backtracking we check if any node has any unvisited adjacent node and if it is there, we make it as visited.
BFS:
Here we visit a node, we insert that node, and all other adjacent nodes to it into the queue. Then while pop the element from queue, we check if there is any unvisited adjacent nodes for the popped out node. By doing so we get to BFS traversal.
Implementation of Graph traversal using Stack[vector] and Queue in C++
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
//recursive function for DFS traversal
/*
* adj [] - Adjacency matrix
* s - Start node
* visited - visited array list
*/
void DFS(vector <int >adj[],int s, bool visited[])
{
visited[s] = true;
cout<<" "<< s;
vector <int >::iterator it;
for(it = adj[s].begin(); it!= adj[s].end(); it++)
if(!visited[*it])
DFS(adj,*it,visited);
}
//recursive function for BFS traversal
/*
* adj [] - Adjacency matrix
* s - Start node
* n - Number of nodes
*/
void BFS(vector <int >adj[],int s,int n)
{
bool visited[n];
memset(visited,0, sizeof(visited));
visited[s] = 1;
queue <int >Q;
Q.push(s);
while(!Q.empty())
{
int v = Q.front();
Q.pop();
cout<<" "<<v;
vector <int >::iterator it;
for(it = adj[v].begin(); it != adj[v].end(); it++)
if(!visited[*it])
{
visited[*it] = 1;
Q.push(*it);
}
}
}
//add edge from source to destination.
void addEdge(vector <int > adj[],int src, int dest)
{
adj[src].push_back(dest);
}
int main(int argc, char const *argv[])
{
int v = 5;
vector<int > adj[v];
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 4, 2);
addEdge(adj, 2, 3);
cout<<"DFS traversal = "<<endl;
bool visited[v];
memset(visited,0, sizeof(visited));
DFS(adj,0, visited);
cout<<endl<<endl;
cout<<"BFS traversal = "<<endl;
BFS(adj,0, v);
cout<<endl<<endl;
return 0;
}
Output:
DFS traversal = 0 1 2 3 4 BFS traversal = 0 1 4 2 3
Further Reading: