In this tutorial we shall look at longest increasing subsequence and we shall solve it by using Dynamic Programming.
Problem Statement:
You are given an array of integers; you need to find the longest increasing subsequence.
It means that, you need to find a sub array in sorted whose sum is max.
Example:
Output:
Here the length is 4.
Here 1, 2, 5, 8 are in sorted order in the array.
There is also 3, 8. But the total sum is less.
So we shall solve this example with help of Dynamic Programming.
We shall take a temp array as below
Now at the least, we can have longest increasing subsequence as 1 at every index. Because, if there are no increasing subsequence in the array, then every index in itself can be a subsequence.
Hence we fill our DP array with all 1 at all the index initially.
To solve this problem, we take 2 variables “i” and “j”. Where “i” starts from index [1] and “j” starts from 0 to “i”.
Now we check if the value at array[j] is less than the value at array[i], then we perform an operation in our DP table, then we increment the index of “j”.
If the value of arr[j] is greater than the value of arr[i], then we don’t do any operation on DP array, we just increment the index of “j”.
When “j” and “i” reaches to the same index, we increment the “i” value to point to next element and reset the “j” value to 0.
And again we continue our previous step.
We shall understand this with help of an example.
Pass 1:
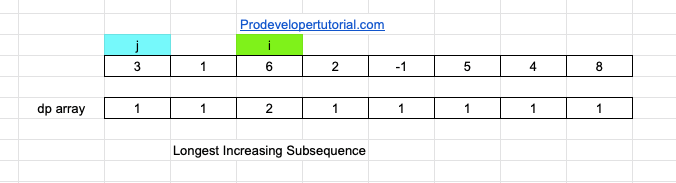
Initial “i” and “j” values are as shown below
Here “j” is not less than i. Hence increment “j”. But, “i” and “j” are in same index. Hence we reset “j” to 0 and increment “i” value as shown below:
Now arr[j] < arr[i]. Hence the longest increasing subsequence at dp[i] will be dp[j]+1.
So it will be dp[2] = dp[0] + 1
dp[2] = 1 + 1
dp[2] = 2
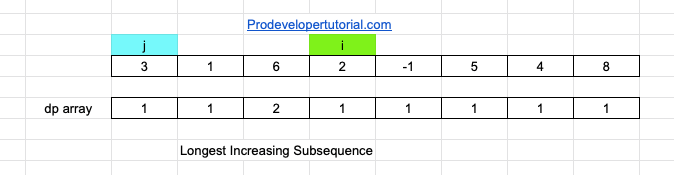
Now increment “j” value. Now also arr[j] < arr[i].
Hence dp[i] = dp[j]+1
= 1 + 1
Now increment “j”, now index of both “i” and “j” are same. Hence increment “i” by 1 and reset j value to 0.
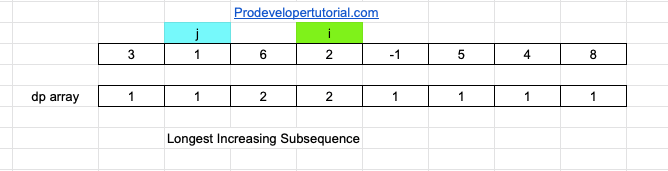
Now arr[j] is not less than arr[i]. Hence increment “j”.
Now arr[j] < arr[i]. hence dp[i] = dp[j] +1
= 1 + 1 = 2
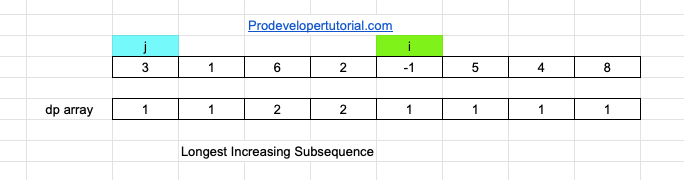
Increment j. Now arr[j] =6 and arr[i] = 2. arr[j] is not lesser than arr[i]. Hence increment “j”. Now that “i” and “j” are at the same index. Increment “i” value, reset j value to 0.
Now arr[j] = 3 ad arr[i] = -1, which is not less. Similarly, all the values are greater than arr[i]. Hence we do nothing in this pass.
The next pass will start as shown below:
If you observe the PD array, it will always show the Longest Increasing Subsequence till that index.
Now arr[j] = 3 and arr[i] = 5. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Again arr[j] = 1 and arr[i] = 5. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Again arr[j] = 6 and arr[i] = 5. Which is greater than arr[i]. Increment “j” index.
Again arr[j] = 2 and arr[i] = 5. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 2 + 1 = 3
Again arr[j] = -1 and arr[i] = 5. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= -1 + 1 = 0
Here we take max of values [2, 2, 3, 0]. “3” is the max value.
At the end of the pass the DP array will look like below:
Again for the next pass, the variables will be as below:
Now arr[j] = 3 and arr[i] =4. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Now arr[j] = 1 and arr[i] =4. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Now arr[j] = 6 and arr[i] =4. Which is greater than arr[i]. Do nothing, increment index of “j”.
Now arr[j] = 2 and arr[i] =4. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 2 + 1 = 3
Now arr[j] = -1 and arr[i] =4. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Now arr[j] = 5 and arr[i] =4. Which is greater than arr[i]. Do nothing, increment index of “j”.
At the end of this pass, the DP array will be as below:
At the beginning of the next pass, the points will be as below:
Now arr[j] = 3 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Now arr[j] = 1 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 1 + 1 = 2
Now arr[j] = 6 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 2 + 1 = 3
Now arr[j] = 2 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 2 + 1 = 3
Now arr[j] = -1 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= -1 + 1 = 0
Now arr[j] = 5 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
=3 + 1 = 4
Now arr[j] = 4 and arr[i] = 8. Which is less than arr[i]. Hence update DP array.
dp[i] = dp[j] + 1
= 3 + 1 = 4
The max value is 4, hence our result.
Solution in C++
#include<iostream>
using namespace std;
int dp_function( int arr[], int n )
{
int dp_array[n];
dp_array[0] = 1;
for (int i = 1; i < n; i++ )
{
dp_array[i] = 1;
for (int j = 0; j < i; j++ )
if ( arr[i] > arr[j] && dp_array[i] < dp_array[j] + 1)
dp_array[i] = dp_array[j] + 1;
}
return *max_element(dp_array, dp_array+n);
}
int main()
{
int arr[] = { 3, 1, 6, 2, -1, 5, 4, 8 };
int n = sizeof(arr)/sizeof(arr[0]);
printf("Length of Longest Increasing Subsequence is %d\n", dp_function( arr, n ) );
return 0;
}
List Of Tutorials available in this website: