In this tutorial we shall solve longest Bitonic subsequence using DP.
Before solving the question, let’s understand what does Bitonic means.
Bitonic is a sequence where the number increases at certain point and decreases from that point.
For example:
Consider the array below
Here if you see the highlighted numbers as shown below:
They are the Longest bitonic subsequence.
What is a Bitonic Point?
A point where the elements are increasing and from that point they decrease is called as bitonic point.
In our example “6” is bitonic point.
Now we shall see how to solve this problem.
We shall take help of Longest Increasing Subsequence technique to solve Longest Bitonic Subsequence. Below are the steps:
- Take Longest Increasing subsequence from Left to Right
- Take Longest Increasing subsequence from Right to Left.
- Take the sum at that index of both the arrays -1. The max value will be the result.
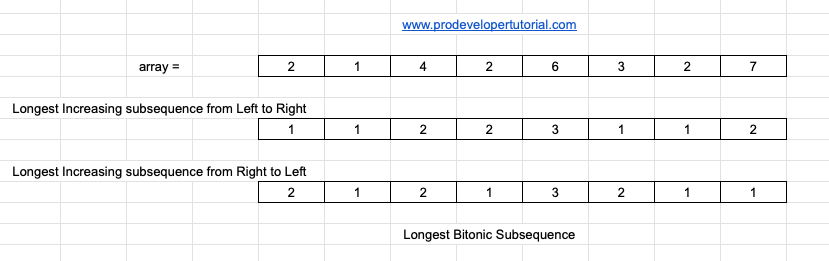
Consider the example:
From the image above, we can get below result:
Hence the longest bitonic subsequence is 5
Solution in C++
#include<iostream>
using namespace std;
/* get_lbs_length() returns the length of the Longest Bitonic Subsequence in
lis_array[i] ==> Longest Increasing subsequence ending with arr[i]
lds_array[i] ==> Longest decreasing subsequence starting with arr[i]
*/
int get_lbs_length( int arr[], int n )
{
int i, j;
//initialize lis_array
int *lis_array = new int[n];
for (i = 0; i < n; i++)
lis_array[i] = 1;
/* Compute LIS values from left to right */
for (i = 1; i < n; i++)
for (j = 0; j < i; j++)
if (arr[i] > arr[j] && lis_array[i] < lis_array[j] + 1)
lis_array[i] = lis_array[j] + 1;
// initialize lds_array
int *lds_array = new int [n];
for (i = 0; i < n; i++)
lds_array[i] = 1;
// Compute LDS values from right to left
for (i = n-2; i >= 0; i--)
for (j = n-1; j > i; j--)
if (arr[i] > arr[j] && lds_array[i] < lds_array[j] + 1)
lds_array[i] = lds_array[j] + 1;
// Return the maximum value of lis_array[i] + lds_array[i] - 1
int max = lis_array[0] + lds_array[0] - 1;
for (i = 1; i < n; i++)
if (lis_array[i] + lds_array[i] - 1 > max)
max = lis_array[i] + lds_array[i] - 1;
return max;
}
int main()
{
int arr[] = {2, 1, 4, 2, 6, 3, 2, 7};
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"Length of Longest Bitonic Subsequence is "<< get_lbs_length( arr, n )<<endl;
return 0;
}