Diameter of a Binary Tree

In this chapter we shall solve how to find out diameter of a binary tree.

Problem statement:

You are given root node of a binary tree, you need to find the diameter in that tree.

Now wait a minute,
Diameter term is usually used in reference to a circle, but how is it possible to use it with tree?

In tree diameter is usually referred to longest path between 2 leaf nodes in the tree.

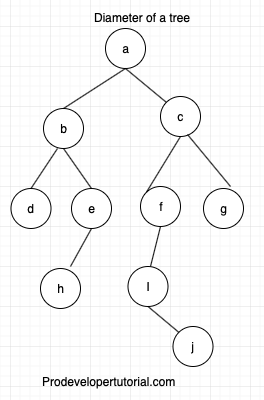
Consider the given example:

Here the diameter is the longest path between 2 leaf nodes is:

h -> e -> b -> a -> c -> f -> i -> j

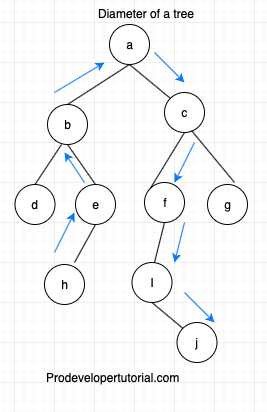
The path is shown in below image

In this tutorial we shall see how to solve.

So from the image above, we ca see that the diameter is equal to [ height of left sub tree + height of right sub tree + 1].

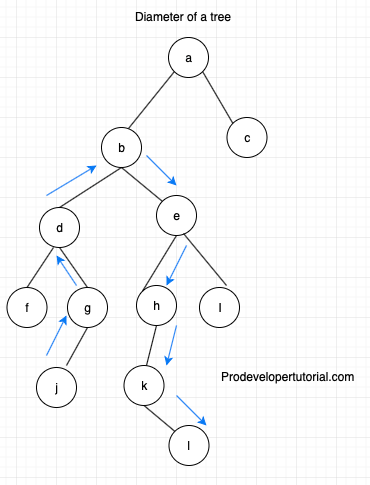
The above formula works if the diameter is passing through the root. What if the diameter is not passing through root as shown in the example below:

In the above image, the diameter will not pass through the root, but rather it will pass through the root of another sub tree.

Hence in this situation, we use the below formula.

Max(left_diameter, right_diameter)

So our full formula will be:

Max(left_height + right_height + 1, max(left_diameter, right_diameter)).

So our function will be as below:

int diameter (node *p)
{
	if (p == NULL)
		return 0;

		int left_height = height(p -> left)
		int right_height = height(p -> right)

		int left_diameter = diameter(p -> left)
		int right_diameter = diameter(p -> right)

		int result = max (left_height+ right_height + 1, max (left_diameter, right_diameter))
}

From the function above,
left_height will calculate the left height
right_height will calculate the right height
left_diameter is used to calculate the left sub tree diameter
right_diameter is used to calculate the right sub tree diameter

Finally, we will arrive at the result.