In this chapter we shall see tree spiral order traversal using 2 stacks.
Problem statement:
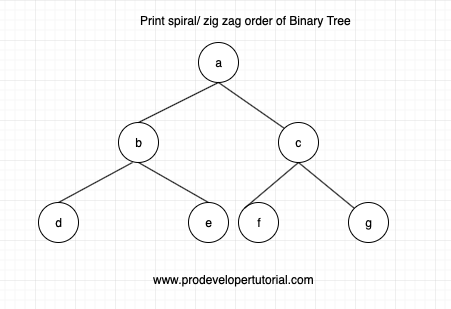
Given a root of the Binary tree, you need to print the nodes in a spiral order.
Consider the tree as below:
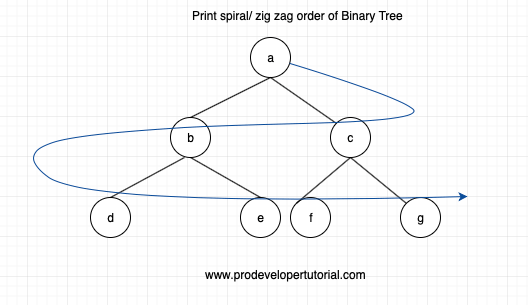
The zigzag order will be as shown below:
The solution will be
A, c, b, d, e, f, g
We can solve this problem with the help of 2 stacks.
The solution using 2 stacks is very simple as explained below:
Step 1: Push node in S1.
Step 2: Insert the children of the root node in s2.
Step 3: Pop s1, now s1 is empty.
Step 4: Go to s2, start popping elements in s2, and add it’s children in S1.
Step 5: Continue step 4 till it is empty.
Step 6: Now again pop from S1 and insert it’s children in S2.
This is kind of recursion. You choose a stack and pop from it and insert it’s children in opposite stack. As we are doing it alternatively, we can print it in spiral order.
Let’s understand the steps with help of example:
So in simple words, when you are popping the element from left stack, insert elements into right stack and vice versa.
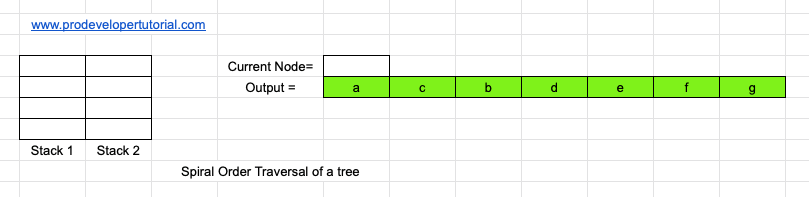
Consider the tree in the example given and consider 2 sacks given below:
First inset “a” root node into stack 1 and the current node and output both are NULL.
Now we shall take it out from stack 1, we need to enter it’s children on stack 2. First enter left child “b” then right child “c” into the stack as shown below:
Now that there are no more elements in stack 1, and we have visited all the children of node “a” we write node “a” into output array
Now that our stack 1 is empty we shall go to stack 2 and pop out the first element into current node. And then add it’s children to stack 1, no this time first right node and then left node as shown below:
Now there are no nodes to visit, we shall write “e” into the output. Then pop “b” into the current node. Then write down it’s children into stack 1. First right child and left child as shown below:
Now print “b” node in output array and now stack 2 is empty, we shall start popping from stack 2.
Note how we go to alternate stack once present stack is empty and insert element to other stack that is not currently chosen. By doing this we can arrive at our result.
As all the nodes are entered on the stack 1 are the leaf node, we can directly copy them into o/p array.
Thus achieving our result.
The final result will look like below:
Hence the result.
Solution in C++
#include <iostream>
#include <stack>
#include <map>
using namespace std;
// structure to hold binary tree node
struct Node
{
int data;
Node *left, *right;
Node(int data)
{
this->data = data;
this->left = this->right = nullptr;
}
};
void perform_zizag_traversal(Node* root)
{
if (!root)
return;
stack<Node*> currentlevel;
stack<Node*> nextlevel;
// push the root
currentlevel.push(root);
// first print left to right
// then right to left
bool direction_left_to_right = true;
while (!currentlevel.empty())
{
struct Node* temp = currentlevel.top();
currentlevel.pop();
if (temp)
{
//print the data
cout << temp->data << " ";
// fill the next level data according to
// the direction
if (direction_left_to_right)
{
if (temp->left)
nextlevel.push(temp->left);
if (temp->right)
nextlevel.push(temp->right);
}
else
{
if (temp->right)
nextlevel.push(temp->right);
if (temp->left)
nextlevel.push(temp->left);
}
}
// if the current level is empty
// change the direction and swap the node
if (currentlevel.empty())
{
//change direction
direction_left_to_right = !direction_left_to_right;
swap(currentlevel, nextlevel);
}
}
}
int main()
{
Node* root = nullptr;
/* Binary tree:
16
/ \
/ \
10 25
/ \ / \
/ \ / \
7 15 18 30
*/
root = new Node(16);
root->left = new Node(10);
root->right = new Node(25);
root->left->left = new Node(7);
root->left->right = new Node(15);
root->right->left = new Node(18);
root->right->right = new Node(30);
perform_zizag_traversal(root);
return 0;
}
Output:
16 25 10 7 15 18 30