Travelling salesman problem with implementation

In this chapter we shall solve Travelling Salesman Problem with help of dynamic programming.

Problem statement:

A salesman will start from a parent city and visit all the cities only once and return to parent city. He has to do it with least cost possible.

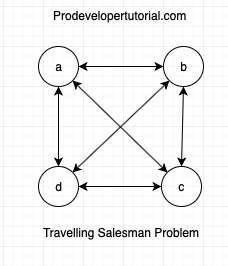
Consider the below graph and let the parent city be “a”.

Now let’s write the valid cases where the salesman visits all the cities only once and return to source city.

a -> b -> c -> d ->a

a -> d -> c -> b ->a

Below are invalid scenarios:

a -> b -> d -> c -> b -> a

Here we have visited “b” 2 times. As you can see from the above valid case, we need to find a Hamiltonian cycle.

 As there can be many routes/cycles, we need to find a path with min cost.

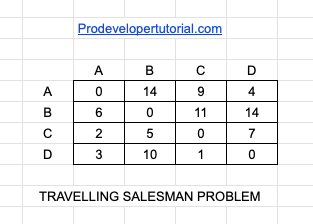
Below is the cost of adjacency matrix.

So this problem can be solved by 3 different methods:

1. 1. Brute force Approach
   2. Dynamic Programming
   3. Branch and Bound approach

In this tutorial we shall follow dynamic programming approach.

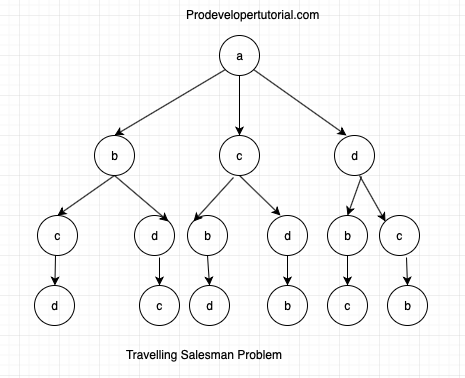
So we shall understand the DP approach with the help of the tree below:

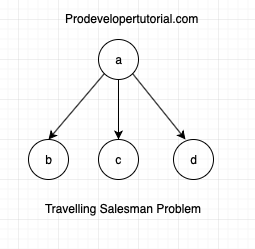
From the given graph, we have chosen “a” as source vertex.

Hence from “a” we can go to “b” “c” and “d”. It can be shown as below:

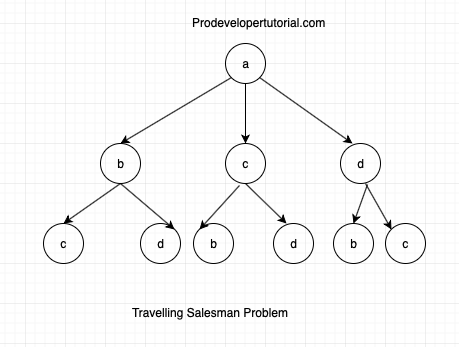
Again from “b” he can go to “d” or “c”

Again from “c” he can go to “b” or “d”

Again from “d” he can go to “b” or “c”

Again from node “c” he go to “c”

Again from node “d” he go to “c”

Again from node “b” he go to “d”

Again from node “d” he go to “b”

Again from node “b” he go to “c”

Again from node “c” he go to “b”

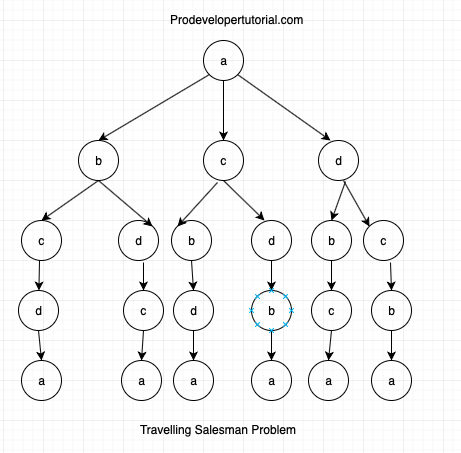
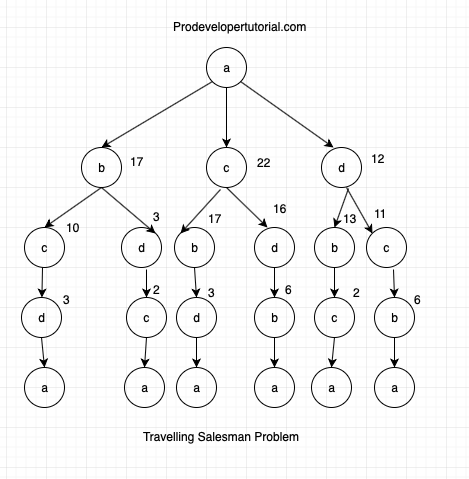
So above image shows all the possible paths. You need to reach to the source vertex again. Hence we can further update the tree as below:

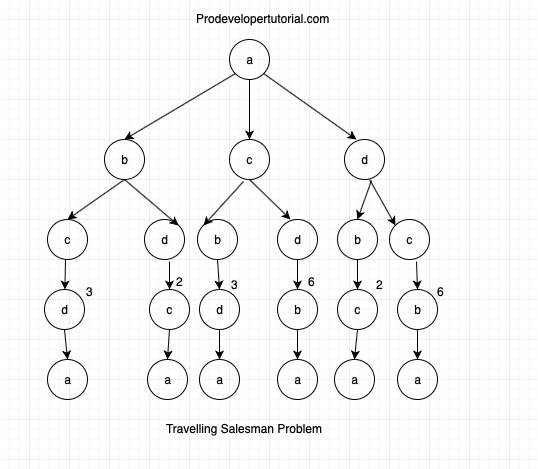
Starting from the last path, we go from bottom to top and update the cost taking from cost table.

So start from “d” to “a”, it is 3

Cost from “c” to “a”, it is 2

Cost from “d” to “a”, it is 3

Cost from “b” to “a”, it is 6

Cost from “c” to “a”, it is 2

Cost from “b” to “a”, it is 6

Again we shall go one level up and find the total distance:

c -> d -> a => i.e c -> d + d -> a=> 7 + 3 = 10

d -> c -> a => d -> c + c -> a => 1 + 2 = 3

b -> d -> a => b -> d + d -> a => 14 + 3 = 17

d -> b -> a => d -> b + b -> a => 10 + 6 = 16

b -> c -> a => b -> c + c -> a => 11 + 2 = 13

c -> b -> a => c -> b + b -> a=> 5 + 6 = 11

The updated tree is as below:

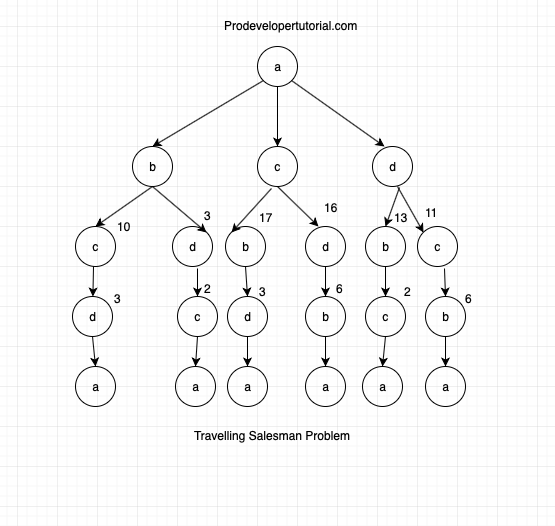
Now again we go one level up, and check the value for “b -> c -> d -> a”, as we have calculated value for “c -> d -> a”, we just need to add that value to the last path. Here with help of DP table we shall be able to do it efficiently.

b -> c + (c -> d -> a) = 11 +10 = 21

b -> a + (d -> c -> a) = 14 +3 = 17

c -> b + (b -> d -> a) = 5 +17 = 22

c -> d + (d -> b -> a) = 7 +16 = 23

d -> b + (b -> c -> a) = 10 +13 = 23

d -> c + (c -> b -> a) = 1 +11 = 12

Now that we have calculated the value for all 6 paths, at the parent node of “b”, “c”, “d”. We have 2 values, we need to find min of 2 values.

For node “b” we have:

b -> c -> d -> a  = 21

b -> d -> c -> a  = 17

Here min is 17, take 17.

For node “c” we have:

c -> b -> d -> a = 22

c -> d -> b -> a = 23

Here min is 22. Take 22.

For node “d” we have:

d -> b -> c -> a = 23

d -> c -> b -> a = 12

Take 12.

The tree will be:

Now we go one last level up and calculate the final path:

a -> b + (b -> d -> c -> a) = 14 + 17 = 31

a -> c + (c -> b -> d -> a) = 9 + 22 = 31

a -> d + (d -> c -> b -> a) = 4 + 12 = 16

The min value is 16. Hence our result.

Hence if the salesman travels the path a -> d -> c -> b -> a, he can visit all the cities only once and arrive at the initial city with min cost.

Implementation of Travelling Salesman Problem using C++

#include <vector>
#include <iostream>
#include <limits.h>
using namespace std;

int tsp(const vector<vector<int>>& cities, int pos, int visited, vector<vector<int>>& state)
{
  if(visited == ((1 << cities.size()) - 1))
  return cities[pos][0]; 

if(state[pos][visited] != INT_MAX)
  return state[pos][visited];

for(int i = 0; i < cities.size(); ++i)
{
  if(i == pos || (visited & (1 << i)))
    continue;

  int distance = cities[pos][i] + tsp(cities, i, visited | (1 << i), state);

  if(distance < state[pos][visited])
    state[pos][visited] = distance;
}
return state[pos][visited];
}

int main()
{
    vector<vector<int>> cities = { { 0, 15, 4, 5 },
                                   { 14, 0, 11, 4 },
                                   { 5, 21, 0, 8 },
                                   { 5, 4, 12, 0 }
                                 };
    vector<vector<int>> state(cities.size());

for(auto& neighbors : state)
        neighbors = vector<int>((1 << cities.size()) - 1, INT_MAX);

    cout << "minimum: " << tsp(cities, 0, 1, state) << endl;
return 0;
}

Output

minimum: 25