Introduction:
This is a very simple algorithm that works if there are only 3 different types of keys in an array.
For example:
If we have an un-sorted array of 0, 1, 2 as shown {2, 0, 0, 1, 1, 2, 0, 2, 1}, easy solution is to count the number of 0’s, 1’s and 2’s then put those many elements inside the array, but this solution is not efficient.
To solve the array in least time complexity then we use “Dutch National Flag” algorithm.
Algorithm Explanation:
In this algorithm, we consider one element will be in the middle. And the elements lesser than the middle element will be moved towards left and the elements greater than the middle element will be moved towards the right side.
Thus automatically the array will be sorted.
Note: The middle element in some context is called as a pivot element. i.e in [0, 1, 2], 1 is the pivot element.
Steps for the algorithm:
Step 1: Set low_index = 0, high_index = n – 1, mid_index = 0; The mid variable is going to trace all the elements in the array.
Step 2: We get a[mid] element and perform below steps Case 0: If a[mid] == 0, Then move to the left, by swapping a[ low_index ] and a[ mid_index ].Then increment low_index and mid_index. Case 1: If a[mid] == 1 [piot element], we don’t do any swapping operation. But we increment mid_index. Case 2: If a[mid] == 2, Then move to the right, by swapping a[ mid_index ] and a[high_index]. Then decrement high_index.
Step 3: Loop till mid_index > high_index.
Note: In Case 2 we are not changing the value of mid_index. That is because the element that got swapped with high_index might be 0. If it is 0, then we have to perform the operation of taking 0 to the left side of the pivot element.
Let us understand this algorithm with help of an example:
Consider the elements given below
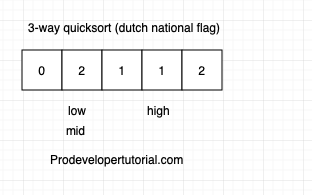
Initially the values will be as shown below:
as arr[mid] = arr[0] = 2, you need to swap are[mid] with are[high] and decrease high index by 1. It is as shown in image below:
Now arr[mid] = are[0] = 0. You need to increment both mid index and low index by 1 as shown below:
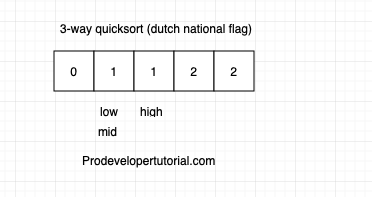
Now arr[mid] = arr[1] =2. Swap arr[mid] with arr[high] and decrement high index as shown below:
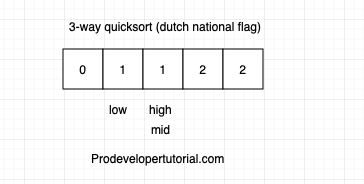
Now arr[mid] = arr[1] = 1. Increment mid index by 1.
Now the mid index == high index. Hence array is sorted.
Algorithm solution in C language.
#include<stdio.h>
void swap(int *num_1, int *num_2)
{
int temp;
temp = *num_1;
*num_1 = *num_2;
*num_2 = temp;
}
void DutchNationalFlagSort(int arr[], int length)
{
int low_index = 0;
int mid_index = 0;
int high_index = length -1;
while(mid_index <= high_index)
{
switch(arr[mid_index])
{
// as we know we are dealing with 0, 1, 2. We take only those cases.
case 0:
swap(&arr[low_index], &arr[mid_index]);
low_index++; mid_index++;
break;
case 1:
mid_index++;
break;
case 2:
swap(&arr[mid_index], &arr[high_index]);
high_index--;
break;
}
}
}
void print_array(int arr[], int length)
{
int itr = 0;
printf("Sorted array is\n");
for (itr = 0; itr < length; itr++)
{
printf("%d ", arr[itr]);
}
printf("\n");
}
int main(int argc, char const *argv[])
{
int arr [100] = {0};
int length = 0;
int itr = 0;
printf("Enter the length of the array\n");
scanf("%d", &length);
for (itr = 0; itr < length; itr++)
{
scanf("%d", &arr[itr]);
}
DutchNationalFlagSort(arr, length);
print_array(arr, length);
return 0;
}
Output:
Enter the length of the array 4 1 2 0 1 Sorted array is 0 1 1 2
Time complexity is O( n ) as we are using only 1 loop.
Further Reading: