Definition:
Selection sort is a sorting technique where the smallest element is taken from the array and placed at the first, same steps are continued for rest of the elements.
Steps for Selection Sort:
1. Get the smallest element from the array list.
2. Exchange it with the first position.
3. Then obtain the second smallest element and exchange it with second position.
4. Continue the steps till all the array elements are sorted.
Selection sort can also be thought as card playing game. We move the cards by choosing smallest card at a time. At any point, we will be having 2 division, where the left hand will have sorted list, right hand will be having un-sorted list.
From the above steps it is evident that we need 2 loops.
1. Outer for loop: It is used to iterate all the array elements one by one.
2. Inner for loop: Here the element from the outer for loop is checked against all the elements from inner for loop. If a smaller element is found, then that element will be replaced with the index of outer for loop.
Below is the pseudo code for the same:
for i <- 0 to n-1 pos <- i for j <- i+1 to n-1 if (arr[j] < arr [pos]) pos = j; end for of j swap arr[i], arr[pos]; end for of i.
Let us understand the working of selection sort using an example:
Consider the array: [4, 6, 1, 34, 21, 14]
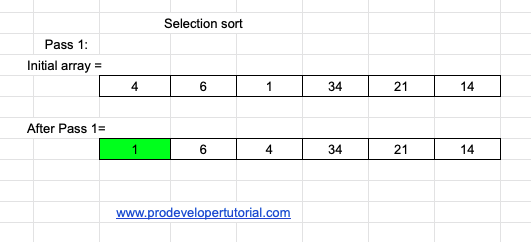
Pass 1:
Initially, we need to fill the index 0, with the smallest element. We first check the array. We see that 1 is the least element and it is in index 2. Hence swap at index 0 and index 2. Below is the result.
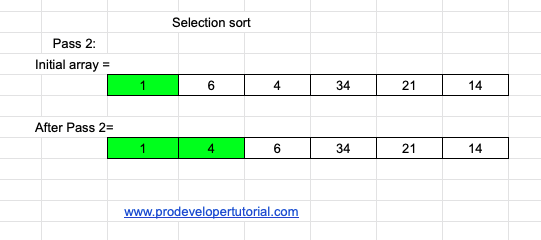
Pass 2:
As we have already placed lowest element in index 0, now we need to place 2nd lowest element.
From the array we can see that 4 is the 2nd lowest element. Hence swap the elements at index 1 and index 2, as shown below:
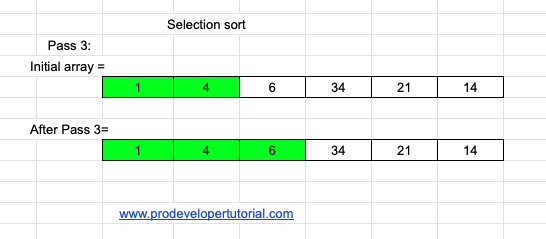
Pass 3:
At pass 3, we can see that element 6 is in it’s correct position. Hence we don’t do anything in this pass.
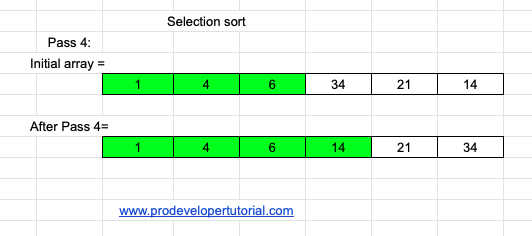
Pass 4:
At pass 4, we swap the elements 34 and 14.
Pass 5 :
As you can see that the array is already sorted. Hence we do nothing.
Selection sort implementation using C language:
#include<stdio.h>
void print_array(int array[], int length)
{
int index = 0;
printf("The sorted array is \n");
for(index = 0 ; index < length ; index++)
{
printf("%d\n",array[index] );
}
}
void swap (int *num_1, int *num_2)
{
int temp = *num_1;
*num_1 = *num_2;
*num_2 = temp;
}
void selection_sort (int array[], int length)
{
int outer_loop_index = 0;
int inner_loop_index = 0;
int position = 0;
for(outer_loop_index = 0; outer_loop_index < length - 1; outer_loop_index ++)
{
position = outer_loop_index;
for(inner_loop_index = outer_loop_index+1 ; inner_loop_index < length ; inner_loop_index ++)
{
if(array [inner_loop_index] < array[position])
{
position = inner_loop_index;
}
}
swap(&array[outer_loop_index], &array [position]);
}
}
int main()
{
int length = 0;
int array[100];
int index = 0;
printf("Enter the length of the array\n");
scanf("%d", &length);
printf("Enter the array elements of length %d\n", length);
for (index = 0; index < length; ++index)
{
scanf("%d", &array[index]);
}
selection_sort(array, length);
print_array(array, length);
}
Output:
Enter the length of the array 5 Enter the array elements of length 5 5 4 3 2 1 The sorted array is 1 2 3 4 5
Running time at worst case for selection sort:
As we are comparing the elements as:
(n-1) + (n-2) + . . . . + 2 + 1
(n(n-1))/2
O(n^2)
Here Best case, worst case, average case is O(n^2).
Further Reading:
Deepak Rajpurohit
selection sort in python-:
#BECAUSE OF INDENTATION PROBLEM I AM WRITING STEPS AS COMMENTS
def selection(arr):
#FIRST LOOP
for i in range(len(arr)):
min = i
#SECOND LOOP FOR COMPARING NEXT #ELEMENTS
for j in range(i+1,len(arr)):
# IF STATEMENT FOR CHECKING THE CURRENT #VALUE IS GREATER THAN NEXT VALUE IF IT IS #WE WILL ASSIGN INDEX TO THE “MIN”.
if arr[i]>arr[j]:
min = j
# NOW SWAP THE VALUES
arr[i],arr[min] = arr[min],arr[i]
# DRIVER CODE
arr=[3,4,6,2,7,1]
selection(arr)
for i in range(len(arr)):
print(arr[i])