In this chapter we shall learn about below topics:
6.1 Big Omega
6.2 Example
6.3 Big Theta Ø
In the previous chapter we learnt about Big O notation, that defines tight upper bound. In this chapter we shall see about Big Omega and Big Theta notation.
6.1 Big Omega Ω:
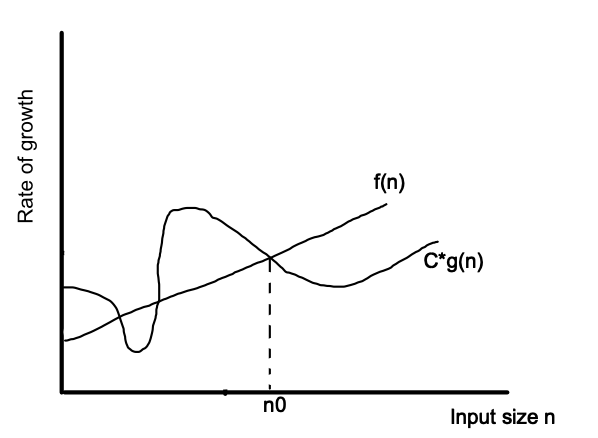
This notation is used to represent tight lower bound. Big omega can be defined as:
For a function f(n) is equal to Ω(g(n)) if there exist a constant C and n0 such that f(n) is always greater than C(g(n)). i.e. f(n) > C(g(n)) or C(g(n)) < f(n).
6.2 Example:
f(n) = 2n + 3 and g(n) = n
Then we need to reduce f(n) to g(n).
Now, when C = 1 we will be able to satisfy the condition.
i.e (2n+3) > (1*n) for all n >=1.
Hence we can say that f(n) is equal to Ω(n).
Hence from the above example we can come to below image.
6.3 Big Theta Ø
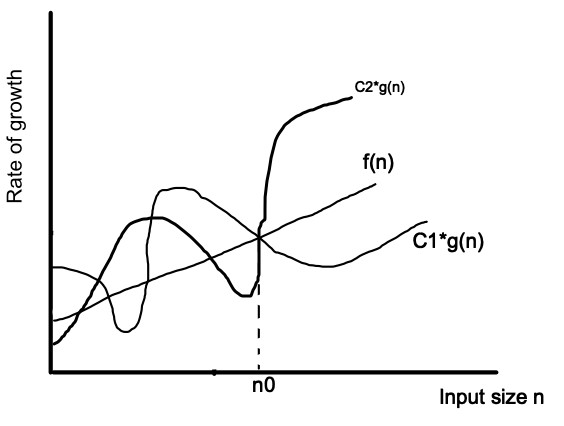
Big theta is used to get the average case for a function. It can be defined as:
For a function f(n) is equal to Ø(n) if a function f(n) is greater than C1 g(n) and is less than C2g(n) for all n>= 0. It means that the function f(n) will always be in-between C1*g(n) and C2*g(n). It can be shown in formula as : C1 g(n) <= f(n) <= C2 g(n).
In other words, if you want to prove big theta, then find out the big O and big Omega separately and you will be able to prove big theta.
Let us take an example and understand Big Theta:
Given f(n) = 5n^2 + 2n + 1
g(n)= n^2
we need to prove C1 g(n) <= f(n) <= C2 g(n)
c1 = 5 and c2 = 8 and n1 = 1
5 * 1 <= (5 (1^2) + 2*1 + 1 <= 8 * 1
Thus proving f(n) = Ø(n^2).
AJ’s guide for DS and Algorithms.Click here to study the complete list of algorithm and data structure tutorial. 85+ chapters to study from.