Find path from top right to bottom left with Solution in C++

A bike is located at the top-left corner of a m x n matrix .

The bike can only move either down or right at any point in time. The bike is trying to reach the bottom-right corner of the matrix.

List the number of unique paths possible.

Example 1:

Input: m = 3, n = 2
Output: 3

Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:
Input: m = 7, n = 3
Output: 28

The solution to this problem can be done in Dynamic Programming.

The fundamental concept too understand is, when you arrive at a point there are only 2 possibilities:

1. Arriving from above. [moving down from the previous point]
2. Arriving from left. [moving right from the previous point].

Let’s analyze by taking a 4 x 4 matrix as an example. It will contain 16 elements in total.

When you are at arr[0][0] position, you can move right to arr[0][1], and from arr[0][1] you can move to right arr[0][2].

Then when you are at arr[0][0] position, you can move down to arr[1][0], and from arr [2][0] you can move down to arr[3][0].

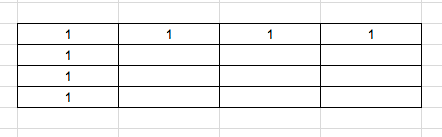
Initial value will be as shown below

So when you come to arr[1][1], you can reach there by 2 ways from top arr[0][1] or from left arr[1][0]. Hence the value will be 2.

From the above we can come to a conclusion for the below equation:

Paths[i][j] = Paths[i - 1][j] + Paths[i][j - 1]

By using the above formula, we can get the final result matrix as below:

1  1  1  1

1  2  3  4

1  3  6  10

1  4  10 20

Finally, we return the value got at the last element i.e. 20.

Solution in C++

/*
* File     : unique_paths.cpp
* Author   : ajay.thousand@gmail.com
* Copyright: @ prodevelopertutorial.com
*/

#include<iostream>
#include<vector>

using namespace std;


int get_unique_paths(int m, int n) 
{
	int path [m] [n];

// Base condition
// initialize first row to 1
	for (int j = 0; j < n; ++j)
	{
		path[0][j] = 1;
	}

// Base condition
// initialize first column to 1
	for (int j = 0; j < n; ++j)
	{
		path[j][0] = 1;
	}

// apply the formula Paths[i][j] = Paths[i - 1][j] + Paths[i][j - 1]

	for (int i = 1; i < m; i++)
    	for (int j = 1; j < n; j++)
        	path[i][j] = path[i - 1][j] + path[i][j - 1];

	for (int i = 0; i < m; i++){
    	for (int j = 0; j < n; j++){
        	cout << path[i][j] <<" ";
    	}
        cout<<endl;
    }

        return path[m - 1][n - 1];
}

int main()
{
	int m = 4;
	int n = 4;

	int result = get_unique_paths(m, n);

	cout<<"The number of unique paths for a "<<m <<" x "<< n<<" matrix is = "<< result<<endl;

	return 0;
}

Output:

The number of unique paths for a 4 x 4 matrix is = 20

List Of Tutorials available in this website: