Introduction to Fenwick tree or Binary Indexed Tree.
In this tutorial we shall lean to perform
- Get range sum
- Update range
by using Fenwick tree.
Problem Statement: Given an array you need to find the sum of ranges.
We need to find the sum for the range [ 0 – 3].
2 + 3 + 1 + 5 = 11.
The simple way to do it by using brute force approach. i.e to add all the elements from the starting index to ending index.
It will take linear amount of time.
Is there any other method to solve this problem?
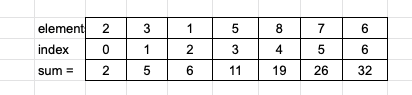
Yes, take another array where you can store the sum of previous index elements.
For example:
But there is a problem here. What if you update the value at index 2, to add “1” to it?
Then you need to add “1” to all the elements after index 2
But if you update at the index ‘0’, then it will take O(n) time to update all the values.
Is there any other efficient method to solve it?
Yes, we can use Fenwick tree.
Fenwick tree is based on the fact that all the numbers can be represented by 2^n. Hence the algorithm will take advantage of this to make queries faster.
We shall understand Fenwick tree with help of an example.
Fenwick tree will be useful for 2 operations. These operations we shall see in this chapter also.
- Compute the sum when given a range
- Add a value an element given an index
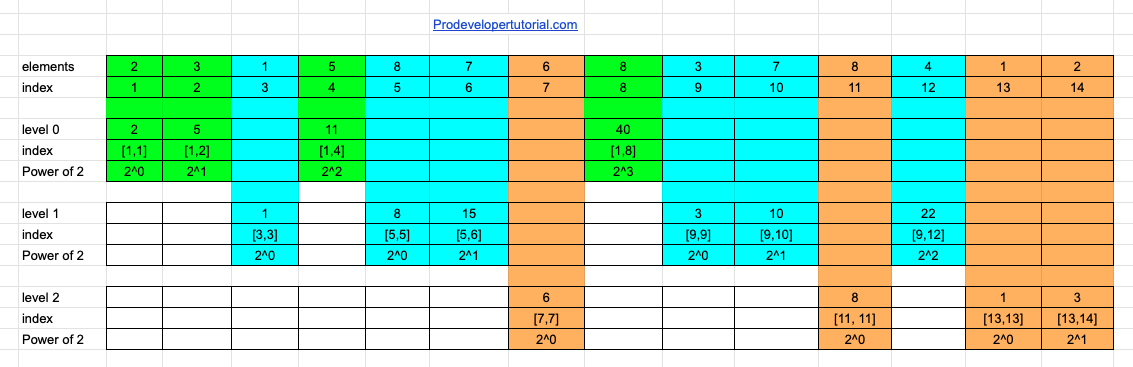
Consider the array with 14 elements as below:
-
Computer the sum when given a range
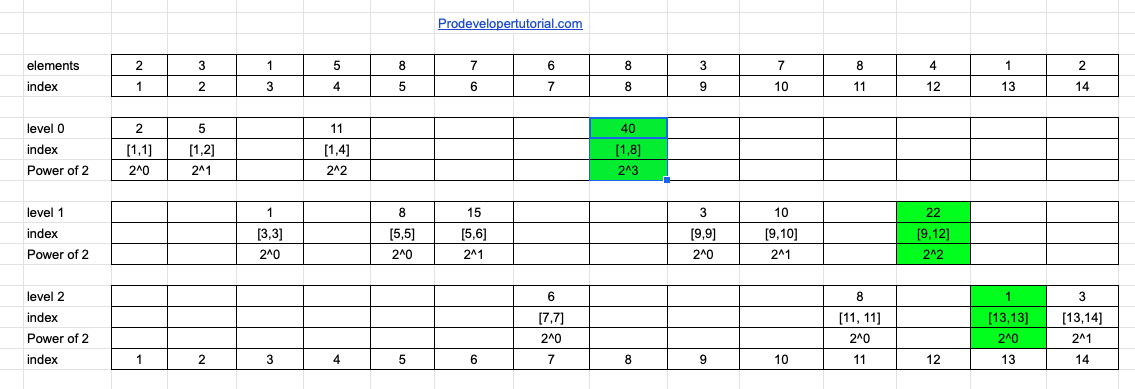
For example we need to find sum(13).
As we said above, any number can be represented with power of 2.
13 can be written as 2^3 + 2^2 + 2^0
13 = Range [1,8] + Range [9, 12] + Range [13,13]
= 40 + 22 + 1
= 63
So what we do is, we have these ranges pre computed. So when we get a range to calculate the sum, we first need to add those pre computed values.
How to pre-compute the values?
We calculate range in power of 2.
Hence the ranges will be 1, 2, 4, 8, 16, 32 …
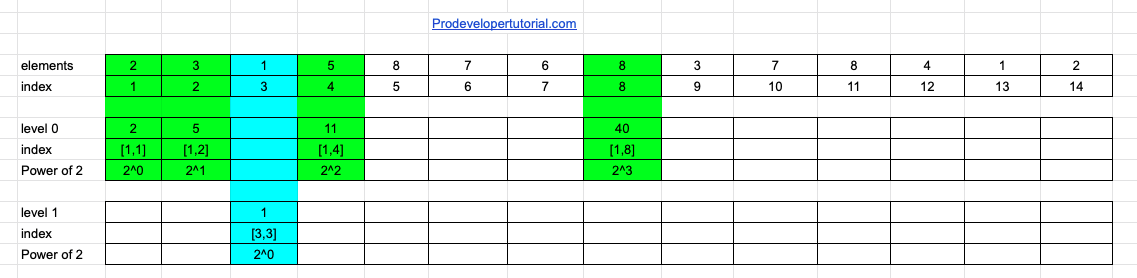
In our example at the first level it can be computed as below
As you can see in the image above, we can infer below 3 points:
- We are calculating the range based on power of 2.
- While we are calculating the range values, there are gaps present
- We stopped at 2^3. Because, 2^4 is 16, that is outside of the range of our array.
So we computed our level 0. Next is level 1, we calculate the same from starting of the gap.
Before doing that, lets mark the index that we have calculated the values for.
While filling the gap, we need to consider the gaps that are continuous.
From the image the index [3, 3] is having only 1 gap. Hence we calculate 2^0 = 1.
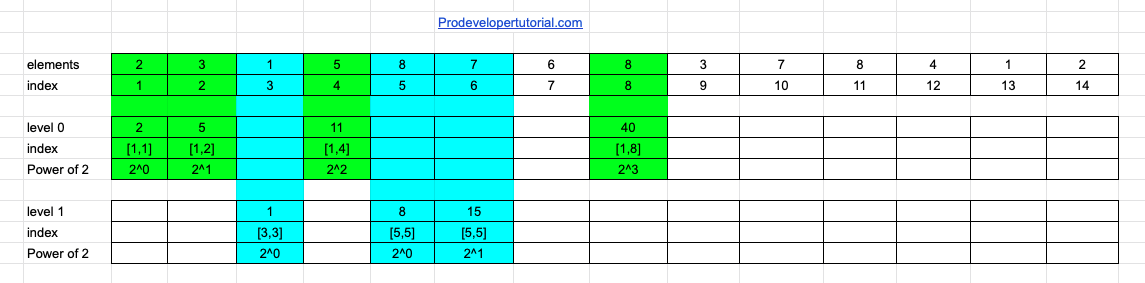
Again the gap starts from the index [5], it is having continuous 3 gaps. Hence we calculate 2^0, 2^1. We don’t need to calculate 2^2 because it’s length is 4 and our gap is not that much long. Hence we leave it there.
Now we look at the index [7, 7] as it is only 1 gap, we calculate only 2^0.
Next gap is from Index 9 to 14. Here again we calculate the value starting from 2 ^0.
Now again we start from index 11. As it is only 1 gap we write as it is.
Next index is 13, the gap is 2. Hence we do 2^0, 2^1 sum range. It can be shown as below:
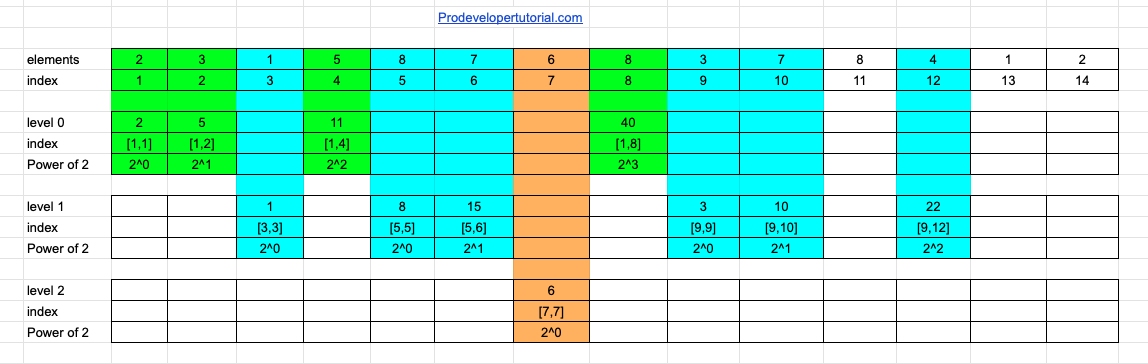
Now that we have covered all the index, we can perform sum range query.
Now we want to know for the sum for range 13. We can write as
Sum (13) = range [1, 8] + range [9, 12] + range [13, 13]/
Now we can calculate easily as shown in image below:
We just need to add the highlighted value and we get our result “63”.
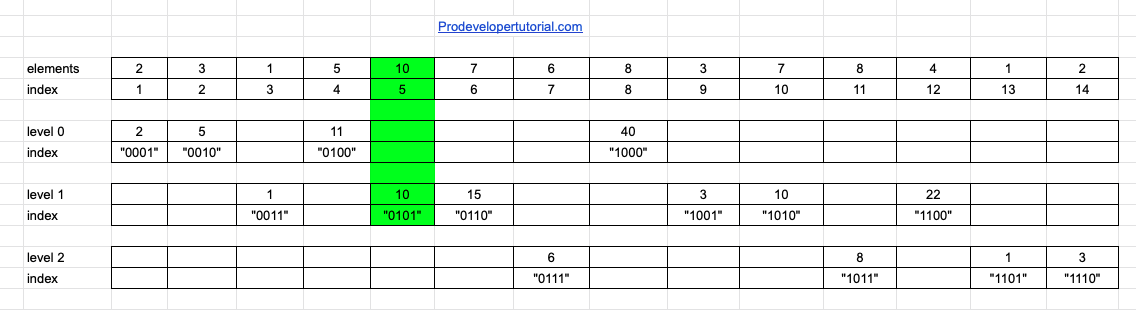
Now how does this actually help us? Let me make it easier for you.
The below image has the index represented as binary numbers
Now the index of the ranges are:
1000 + 1100 + 1101
If you observe the index of 13 in binary is “1101”. When you flip the last digit “1” to “0”, you get the next index to be added i.e. “1100”. Now again you flip the last “1” to “0”, you get “1000” the index next number to add.
How to remove last set bit:
Get the last set bit by doing x & (-x)
Then remove the last set bit by x –x ( x &(-x))
In our example:
X = 13 = 00001101
-X = -13 = 11110011
X & -X = 00000001
X – ( X & (-X)) = 00001100
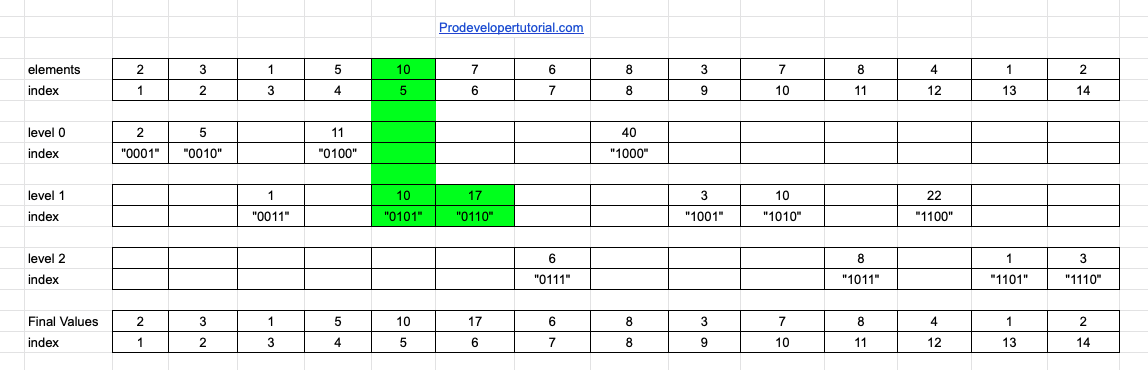
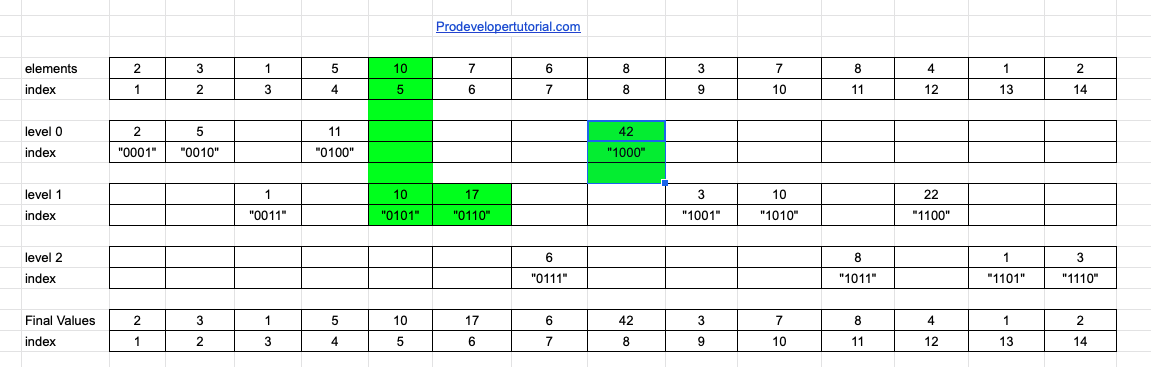
Now we add an element at the given index.
Suppose we are given add 2 to index 5.
Starting from index 5 add 2. If we are not using Fenwick tree, we need to add 2 to all the ranges starting from index 5.
But as we have Fenwick tree constructed, we shall see how to do it.
For the index 5, first we add 2 to element at index 5
Then we shall update all the ranges that are right side to index 5. As we have only one range [5, 6] we update that.
After the index 6, there is no continuous range related to 5. Hence we go one level up and update all the ranges.
Now we go to index 8 and update the value with 2.
Hence we finished our updating values.
Now let’s look how we can achieve this by binary representation:
First we go to “5” i.e 0101, then we go to 0110, from there we go to 1000.
Basically we add the last set bit to know the next index to be updated.
Programmatically it can be achieved as below:
Get the last set bit by doing x & (-x)
Then add the last set bit by x + x ( x &(-x))
Implementation of Fenwick Tree in C
#include <stdio.h>
int FWtree[100] = {0};
int SIZE;
int get_sum(int i)
{
int sum = FWtree[i];
while(i)
{
i -= (i & (-i));
sum += FWtree[i];
}
return sum;
}
void add(int i, int value)
{
while(i < SIZE)
{
FWtree[i] += value;
i += (i & (-i));
}
}
void init_fw_tree(int my_array[], int start, int end)
{
SIZE = end-start+2;
for(int i = 1; i <= end-start+2; i++)
{
add(i, my_array[ start+i-1 ]);
}
}
int main()
{
int my_array[] = {1, 3, 2, 4, 5 ,8, 6, 5 ,0, 3, 4, 3, 2, 2};
init_fw_tree(my_array, 0, 13);
//get sum of all the numbers in the array
printf("The sum of all the numbers in the array is = %d\n",get_sum(14));
// update 5th index with value 8
add(5,8);
printf("The new sum after updating 5th index with value 8 is = %d\n",get_sum(14));
return 0;
}
Output:
The sum of all the numbers in the array is = 48 The new sum after updating 5th index with value 8 is = 56
Further Reading: