Quick Sort is a divide and conquer technique. Usually we use Quick Sort on a very large data set.
Below is a brief on how this algorithm works:
Divide: Divide the array into 2 arrays based on a pivot element.
Conquer: Sort the left array recursively and right array recursively.
Combine: Combine both sorted left and right array.
To perform Quick sort, we need the help of “pivot element”. Pivot element holds an important role in this algorithm.
Steps to perform Quick Sort:
Step 1: The first step is to get a pivot element.
Step 2: Once we get the pivot element, then we create 2 half such that, the elements left to the pivot element are lesser than pivot element. The elements right to pivot element are greater then that of pivot element.
Step 3: We do Step 1 and Step 2 recursively till the array is sorted.
Steps to select pivot element:
As we discussed earlier that selecting “pivot element” is important step in this algorithm.
Step 1: We shall select lowest index as the pivot element.
Step 2: According to the pivot element, we swap the elements in their respective positions.
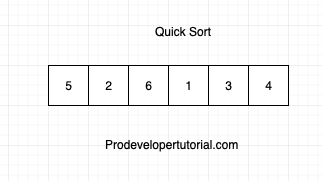
Let us understand Quick Sort with the help of an example:
In this example, we shall select the lowest element as pivot element.
Below are the points to be remembered while doing quick sort:
We take 2 variables, one pointing to the left end of the array and another pointing to the right end of the array.
Then while comparing with the left pointer, we check if the element is less than the pivot element. If it is less, we do nothing. If the element is greater than the pivot element we swap the elements.
Similarly, while comparing with the right pointer, we check if the element is greater than the pivot element. If the element is less than the pivot element, we swap the elements.
By doing the above 2 operations, we make sure that all the elements to the left of pivot element are less and elements to right of pivot are greater. [Revisit these points once you go through the example below].
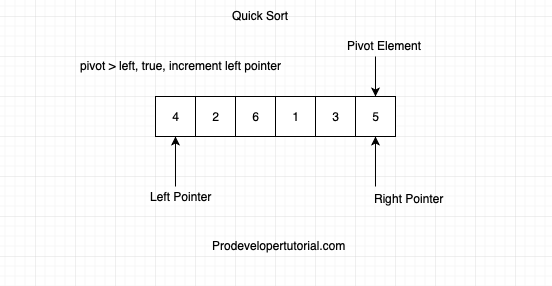
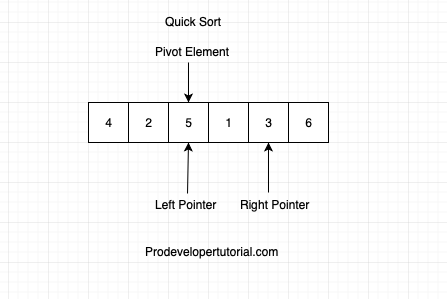
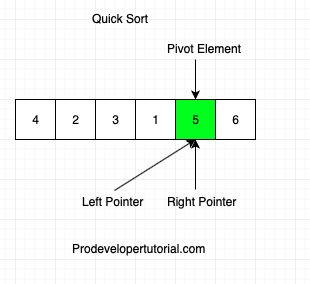
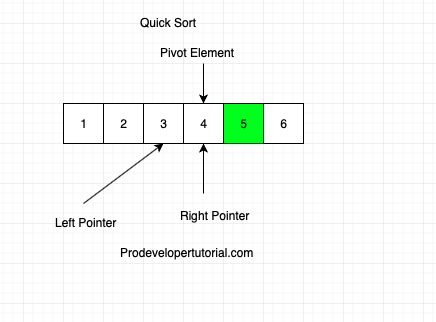
Consider the below array:
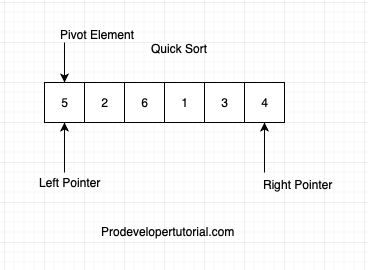
Initially the left pointer will be pointing to left part of the array.
Right pointer will be pointing to the right part of the array.
Pivot element also will be pointing to the left part of the array, as shown below:
We know that, all the elements to the right of the pivot element should be greater than the pivot element and all the elements left of the pivot will be lesser than the pivot element.
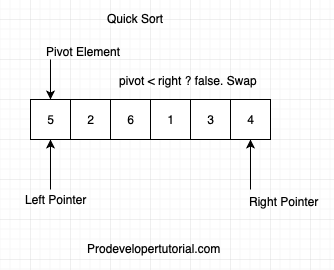
Initially, the pivot is at the left, hence we start comparing from the right and move towards left. To move an element towards left, that element should be less than the pivot element. Hence we check below condition.
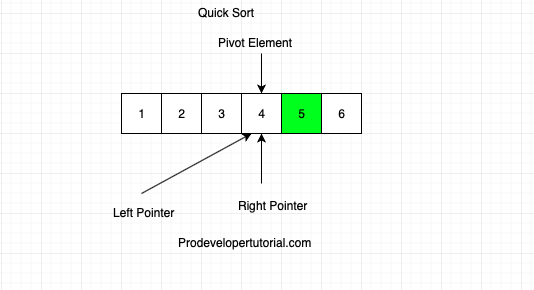
First, we check if arr[pivot] < arr[right]? False.
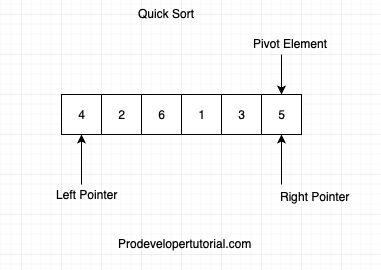
Hence swap pivot and right element.
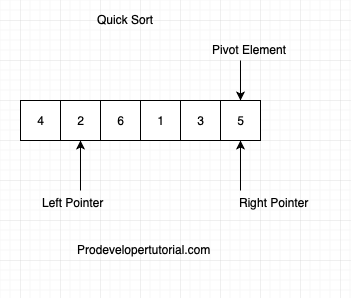
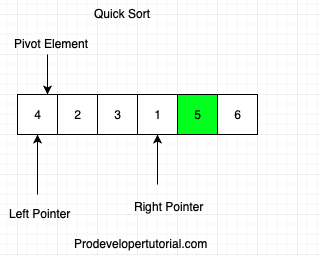
after swap, the pivot element will reach at the end.
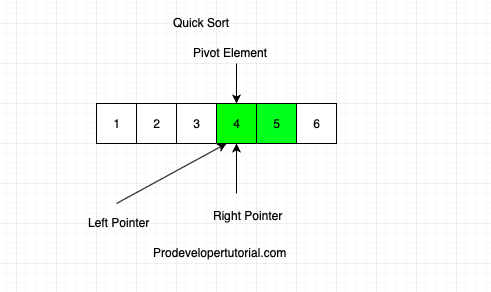
Now that the pivot element is at the right, we start comparing from left and move towards right. For an element to be at right of pivot element, it should be greater than the pivot element. hence we check below condition:
if arr[pivot] > arr[left]? True.
Hence we move the left pointer to the next element as shown below:
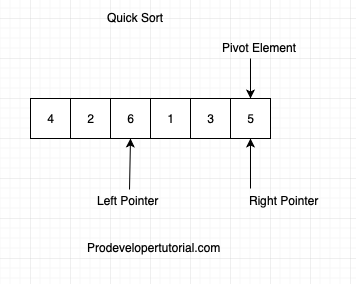
after comparing:
again check if arr[pilot] > arr[left], if(5 > 2) true. Hence increment left pointer to next index as shown below:
Now agin, check if arr[pilot] > arr[left], if(5 > 6) false. Hence swap element 5 and 6.
Now check if arr[pilot] < arr[right], if(5 < 6) true. Decrement right pointer as shown below:
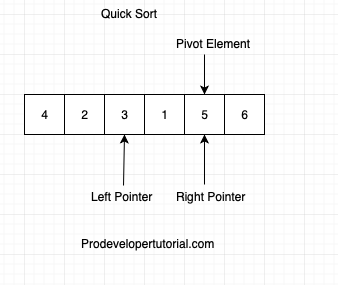
Now again check if arr[pilot] < arr[right], if(5 < 3) false. Hence swap pivot element and right element as shown below:
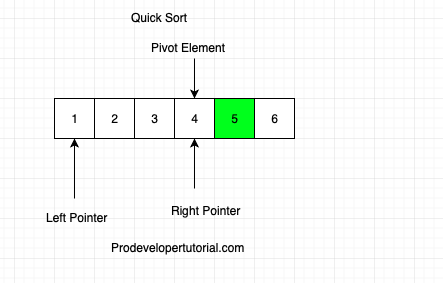
As the pivot element moved from left to right, we start comparing from left and pivot element.
check if arr[pilot] > arr[left], if(5 > 3) true. Increment left pointer
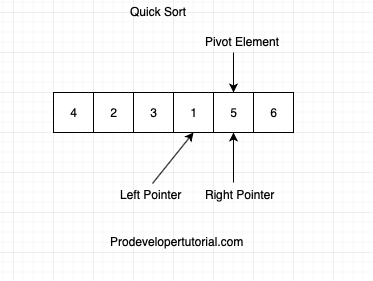
again check if arr[pilot] > arr[left], if(5 > 1) true. Increment left pointer.
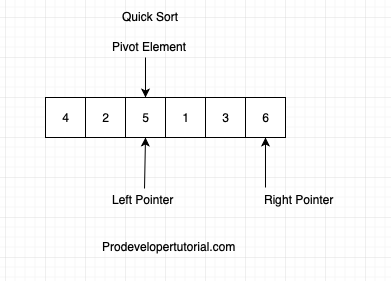
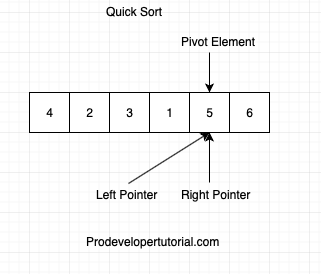
Now that left and right pointer are pointing at the same element of the array, the element 5 is at the pivot element and is in the sorted position.
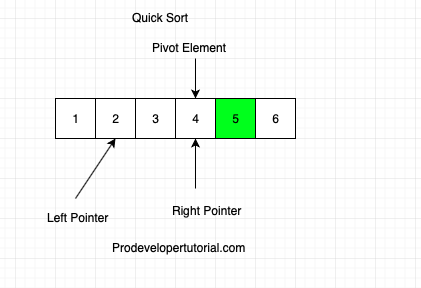
All the elements left of 5 are smaller and elements to right are larger than 5 as shown below:
Again we shave to sort the left part and right part. Again the initial array will be like below:
as the pivot is at left, we compare with right pointer and move towards left.
Hence check if arr[pilot] < arr[right], if(4 < 1) False. Hence swap pivot and right element.
Now check if arr[pilot] > arr[left], if(4 > 1) true. Increment left pointer.
again check if arr[pilot] > arr[left], if(4 > 2) true.Increment left pointer by 1.
again check if arr[pilot] > arr[left], if(4 > 3) true.Increment left pointer by 1.
As both left and right pointer points to the same index, it means that element 4 is at it’s correct position.
Hence again do the same quick sort for the left sub array “1, ,2 , 3”.
Finally we get our sorted array.
C program for Quick Sort is as below:
#include<stdio.h>
void print_array(int array[], int length)
{
int index = 0;
printf("The sorted array is \n");
for(index = 0 ; index < length ; index++)
{
printf("%d\n",array[index] );
}
}
void swap (int *num_1, int *num_2)
{
int temp = *num_1;
*num_1 = *num_2;
*num_2 = temp;
}
int partition(int array[], int lower_index, int upper_index)
{
int pivot = lower_index;
int i = lower_index;
int j = upper_index;
while(i < j)
{
while(array[i] <= array[pivot] && i < lower_index)
i++;
while(array[j] > array[pivot] )
j--;
if(i < j)
{
swap(&array[i], &array[j]);
}
}
swap(&array[pivot], &array[j]);
return j;
}
void quick_sort (int array[], int lower_index, int upper_index)
{
int partition_index = 0;
if(lower_index < upper_index)
{
partition_index = partition(array, lower_index, upper_index);
quick_sort(array, lower_index, partition_index - 1);
quick_sort(array, partition_index + 1, upper_index);
}
}
int main()
{
int length = 0;
int array[100];
int index = 0;
printf("Enter the length of the array\n");
scanf("%d", &length);
printf("Enter the array elements of length %d\n", length);
for (index = 0; index < length; ++index)
{
scanf("%d", &array[index]);
}
quick_sort(array, 0, length-1);
print_array(array, length);
}
Output:
Enter the length of the array 5 Enter the array elements of length 5 5 4 3 2 1 The sorted array is 1 2 3 4 5
Running time at worst case for Quick sort:
The worst case will be achieved when the pivot element is the largest or the smallest element in the array.
Hence for the worst case
T(n) = partition(n) + T(n-1)
==> T(n-2) + T(n-1) + n
==>n(n-1)/2
==>n^2
Hence at worst case, the time consumed will be O(n^2).
Further Reading:
Atul
I tried your code and it is working fine for 10 numbers. Above that it is not printing the sorted array.Can you explain why it is happening?
prodevelopertutorial
I’ll check and inform you