Mnimum Spanning Tree tutorial 1. Introduction to minimum spanning tree

First thing to understand is that this topic will come under Graphs not trees.

Before solving questions related to Minimum Spanning Tree [MST], we shall take a look on what are MST?

In Minimum Spanning Tree, there is a sub part Spanning Tree.

Spanning Tree Introduction:

Given a connected undirected graph, a spanning tree of that graph is a sub graph that has all the vertices and also a tree.

Means, a spanning tree should be connected [connected to all the vertices], acyclic [should not have any cycle] and should have all the vertices.

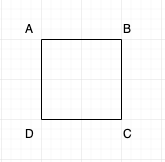
Below is a simple graph

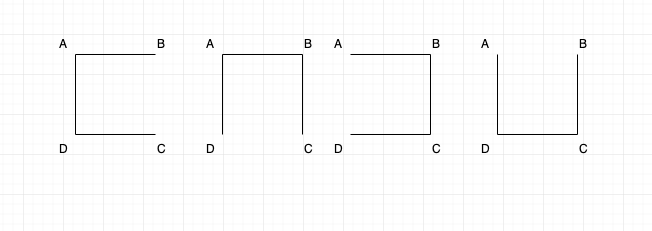
Below are the different number of spanning tree for that graph.

Note:

If there are “n” vertices, then a spanning tree should have “n-1” edges. In the above image, we have 4 vertices, hence our spanning tree has “4 -1 = 3” edges.

Then what is Minimum Spanning Tree?

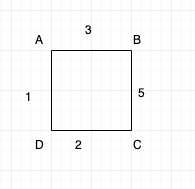
Consider the below weighted graph:

Now you are a sales person, and let us consider each vertices as cities, and you need to visit all the places with minimum amount possible.

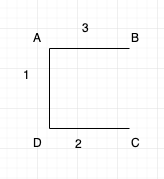
Below image is the solution for it.

So where do we use MST?

We use MST in

1. Network Design
2. Maps
3. Face Verification

In the next MST problems, we shall look at more complex problems with cycle and how to solve them using Prims and Kruskal’s algorithm.

Further Reading:

AJ’s definitive guide for DS and Algorithms. Click here to study the complete list of algorithm and data structure tutorial. 85+ chapters to study from.

List Of Tutorials available in this website: