In this tutorial we shall learn about Prim’s algorithm is used to find MST. This is a greedy based approach.
Below are the conditions for Prim’s algorithm to work:
- The graph should be connected
- Graph should be undirected.
- Graph should be weighted.
The working of Prim’s algorithm is very simple and can be understood by below steps:
- Mark all the nodes as unreached.
- Start from any node, think it as root node and mark that node as reach.
- Generally, node with at least number of vertex should be chosen at first.
- Then find an edge with min cost that connects a reached node and an un-reached node.
- Make unreached node as reach.
- Repeat step 4 and 5 till al the nodes in the graph are reached.
Understanding Prim’s algorithm with the help of an example:
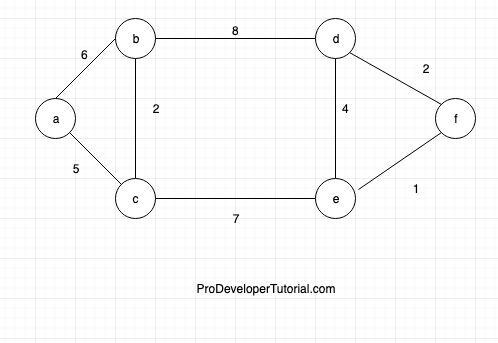
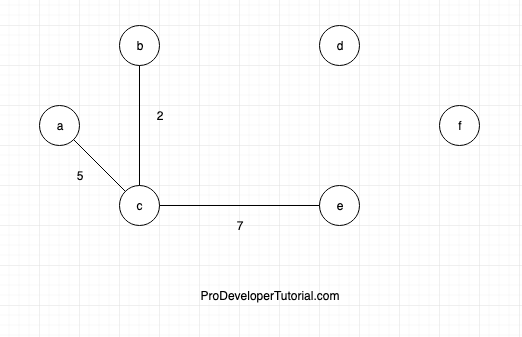
Consider the below graph
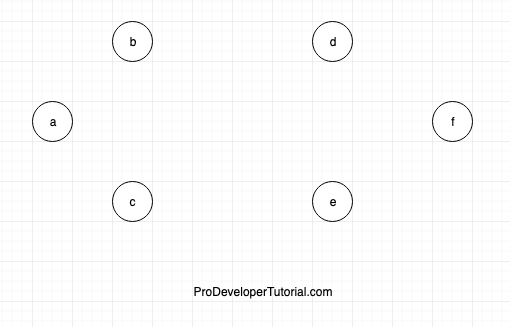
Initially the graph will be empty with no edges connected
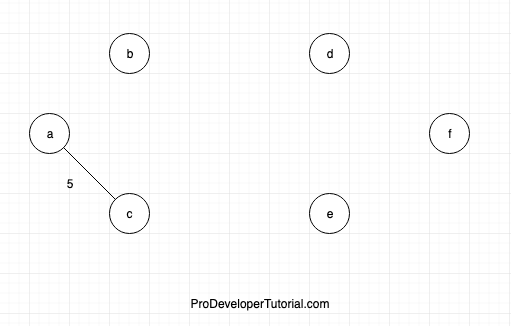
Now start from vertex ‘a’, connect ‘a’ and ‘c’ as it has less weight when compared to ‘a’ and ‘b’
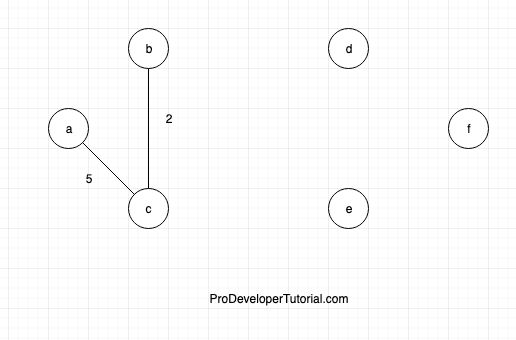
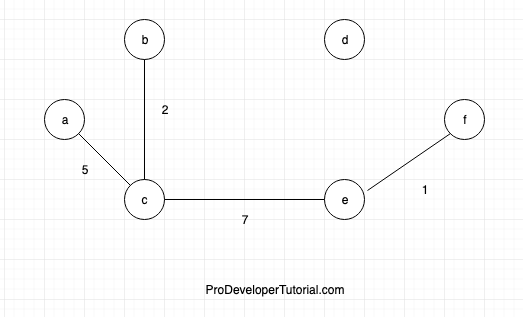
Now go to node ‘c’, and connect node ‘c’ and ‘b’
Now connect ‘c’ and ‘e’ as they are having next lowest weight.
Now connect ‘e’ and ‘f’
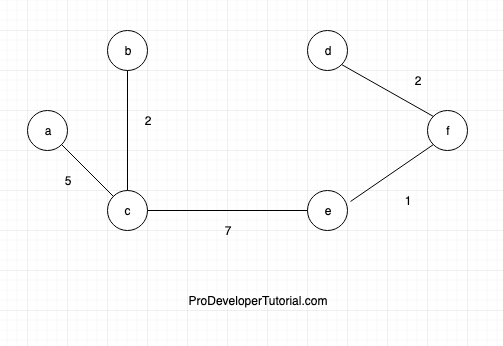
Now connect ‘f’ and ‘d’. Hence we got our minimum spanning tree.
Implementation of Prim’s algorithm
#include <iostream>
#include<vector>
#include<queue>
#define INF 0x3f3f3f3f
using namespace std;
void addEdge(vector<pair<int,int> >adj[],int src,int dest,int weigth)
{
adj[src].push_back(make_pair(dest,weigth));
adj[dest].push_back(make_pair(src,weigth));
}
void PrimsMST(vector<pair<int, int> > adj[],int src,int v)
{
priority_queue<pair<int,int> , vector<pair<int,int> > ,greater<pair<int,int> > >pq;
vector <int >key(v,INF);
vector <int> parent(v,-1);
vector <bool> inMST(v,false);
key[src] = 0;
pq.push(make_pair(0,src));
while(!pq.empty())
{
int u = pq.top().second;
pq.pop();
inMST[u] = true;
vector <pair<int,int> >::iterator it;
for(it = adj[u].begin(); it!= adj[u].end();it++)
{
int v = (*it).first;
int w = (*it).second;
if(inMST[v] == false && key[v] > w)
{
key[v] = w;
pq.push(make_pair(key[v],v));
parent[v] = u;
}
}
}
for(int i=1;i<v;i++)
printf("%d - %d\n",parent[i],i);
}
int main(int argc, char const *argv[])
{
int v = 9;
vector<pair<int,int> >adj[v];
addEdge(adj,0, 1, 2);
addEdge(adj,0, 7, 4);
addEdge(adj,1, 2, 4);
addEdge(adj,1, 7, 9);
addEdge(adj,2, 3, 6);
addEdge(adj,2, 8, 2);
addEdge(adj,2, 5, 4);
addEdge(adj,3, 4, 5);
addEdge(adj,3, 5, 12);
addEdge(adj,4, 5, 8);
addEdge(adj,5, 6, 2);
addEdge(adj,6, 7, 1);
addEdge(adj,6, 8, 6);
addEdge(adj,7, 8, 5);
PrimsMST(adj,0,v);
return 0;
}
Output:
0 - 1 1 - 2 2 - 3 3 - 4 2 - 5 5 - 6 6 - 7 2 - 8
Time complexity of Prim’s algorithm is O(logV)
Prim’s algorithm should be used for a really dense graph with many more edges than vertices.
Kruskal vs Prim’s algorithm:
In krushkal algorithm, we first sort out all the edges according to their weights. Then we start connecting the edges starting from lower weight to higher weight.
In prims algorithm, we start from any node, then we check the adjacent nodes weight. Then we start connecting with the edges with least weight.
Further Reading: