In this chapter we shall learn about below topics:
- What is dynamic programming
- Top down and bottom up approach
- Memonization and tabular method.
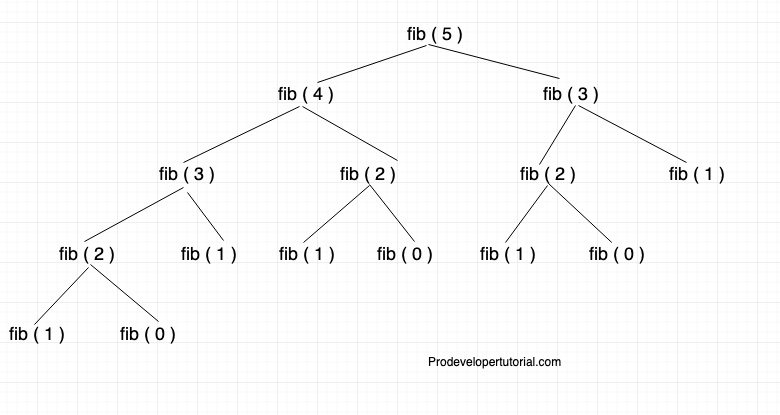
In the previous chapter, we studied about recursion and saw recursion tree as below:
From the above, the time complexity will be 2^n and it you observe carefully we are repeating the calculation for the values that are already been calculated.
We are calculating the values for “fib(2)” “fib(1)” “fib(0)” for more than one time.
So is there a way to calculate them for only once?
Yes, there is a way. We store the result for already calculated value in an array.
Next time when we try to calculate the value for already calculated value, we check in our array if the value is present or not. If present, then we take from the array and use it. Else we calculate the value and store it in the array for further use.
As we are storing the result for already calculated value, for it ca be used in further in our problem is called as dynamic programming.
There are 2 approaches of dong dynamic programming.
- Top down approach / Memonization
- Bottom up approach / Tabular method.
Before we discuss about Topdown and Bottom Up approach, let us discuss about characteristics of Dynamic Programming
Characteristics Of Dynamic Programming
There are 2 most important characteristic of DP, they are:
- Overlapping Subproblems
- Optimal Substructure Property
1. Overlapping Subproblems
a. Any problem can be divided into sub problems.
b. If the sub problem are overlapping i.e solving a sub problem involves in solving the same subproblem multiple times, then that problem will satisfy overlapping subproblem condition.
For example:
For fibonacci series, to find fib(5), we arrive at sub problem tree as mentioned below. If you can see fib(2) is calculated multiple times, fib(1) is also calculated multiple times.
2. Optimal Substructure Property
In this type, the solution can be derived form a simple equation.
For fibonacci series: Fib(n) = Fib(n-1) + Fib(n-2)
-
Top down approach / Memonization
Let us understand this approach by using the same Fibonacci number as an example:
In this approach we take an array to store the values that are previously been calculated.
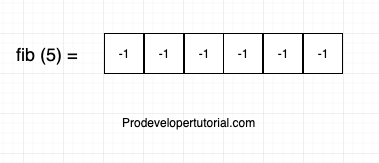
Step 1: Take an array and initialize with -1. As we are calculating for fib( 5 ), we take 5 element array.
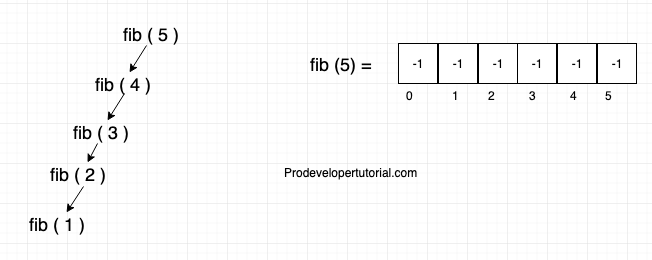
First we calculate for “fib ( 5 )”. The value of fib ( 5 ) is -1, we calculate further, hence make a recursive call to “fib ( 4 )”
Check the 4thindex of the array, it is -1, make a recursive call for “ fib ( 3 )”
As “fib ( 3 )” is also -1, make a recursive call again to “fib ( 2 )”.
As “fib ( 2 )” is also -1 call for “fib ( 1 )”.
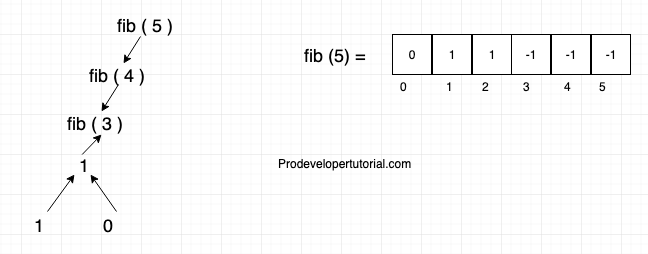
As the index is “1” we return 1 and update the array with 1 for index 1.
Again “fib ( 2 )” will call “fib ( 0 )”. As “0” will return “0” update the array.
Now we can calculate the value for fib ( 2 ) = fib ( 1 ) + fib ( 0 ) = 1 + 0 = 1, update it the array.
Now we have to make 2ndrecursive call to “fib ( 3 )”.
i.e “fib ( 2)”. But as we have already know the value of fib ( 2 ) form the array, we use that value to calculate fib ( 3 ).
Now we need to make 2ndrecursive call to “fib ( 4 )”.
The 2ndrecursive call to “fib ( 4)” is “fib ( 2 )”. We know the value of fib ( 2), we can calculate the value for “ fib ( 4)” and update the array.
Now make 2ndrecursive call for fib ( 5 ). The 2ndrecursive call for “fib ( 5)” is “fib ( 3)”. As we already know the value for fib ( 3), use it and get the final result.
Hence as you can see, by using Memonization approach, we have reduced the time complexity from 2 ^n to O ( n) by using dynamic programming;
And, here we have solved the problem from top to bottom to get the result. This is called as top down approach. We have stored intermediate result in an array. This is called as Memonization technique.
C++ program to find Fibonacci series using Top Down approach with Memonization technique.
#include<iostream>
using namespace std;
int array_memo [6];
int fib(int n)
{
if (array_memo[n] == -1)
{
if (n <= 1)
array_memo[n] = n;
else
array_memo[n] = fib(n - 1) + fib(n - 2);
}
return array_memo[n];
}
int main ()
{
int n = 5;
//initialize array to -1
for(int i = 0; i < 6 ; i++)
array_memo [i] = -1;
cout << "Fibonacci number is " << fib(n)<<endl;
return 0;
}
Output:
Fibonacci number is 5
-
Bottom up approach / Tabular method.
Now we shall learn about bottom up or tabular method.
Tabular method can be achieved by iterative method instead of recursive method. Below is the function that calculate Fibonacci in iterative method.
int fib ( n)
{
int arr[5]
arr[0] = 0
arr[1] = 1
if (n <= 1)
return n
for(i = 2; i <= n ; i++)
{
arr[i] = arr[i-1] + arr [i -2]
}
return arr[n]
}
In the above program, we have to generate an array, and we shall start filling the array from lower index to upper index. As first 2 index are prefilled we shall start with
Pass 3: arr [0] = 0 arr[1] = 1 arr [2] = arr [0] + arr [1] = 1 + 0 arr[2] = 1 array: 0, 1, 1, 0, 0, 0 Pass 4: arr [3] = arr [2] + arr [1] = 1 + 1 arr[2] = 2 array: 0, 1, 1, 2, 0, 0
Pass 4: arr [4] = arr [3] + arr [2] = 2 + 1 arr[4] = 3 array: 0, 1, 1, 2, 3, 0
Pass 5: arr [5] = arr [4] + arr [3] = 2 + 3 arr[4] = 5 array: 0, 1, 1, 2, 3, 5
Here if you observe carefully, we are filling from lower index to higher index. Hence it is bottom up approach using tabular method.
C++ program to find Fibonacci series using Tabular technique.
#include<iostream>
using namespace std;
int fib(int n)
{
int fib_arr[n+1];
fib_arr[0] = 0;
fib_arr[1] = 1;
for (int i = 2; i <= n; i++)
fib_arr[i] = fib_arr[i-1] + fib_arr[i-2];
return fib_arr[n];
}
int main ()
{
int n = 5;
cout<<"Fibonacci number is = "<<fib(n)<<endl;
return 0;
}
Output:
Fibonacci number is = 5
Further Reading: