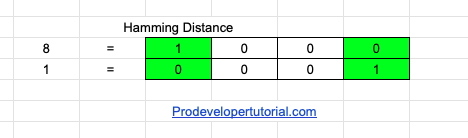
You are given 2 integers, and you need to return the count at which the bits are different in their binary form.
Consider 8 and 1
As highlighted in the image, there are 2 positions where the bits are different. Hence output should be 2.
We shall solve this by bit manipulation.
Before solving the problem, we need to understand 2 concepts
- XOR
- Brian Kernighan’s Algorithm
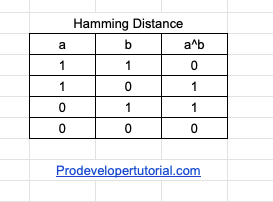
- XOR
The truth table of xor is as below:
As you can see that XOR returns true if 2 bits are different. When 2 bits are same it will return 0. This is what we need for our solution.
Now that when we XOR 2 numbers, we get numbers of set bits that are different in their binary form.
Now we need to calculate/count the number of set bits.
This can be achieved by using Brian Kernighan’s Algorithm.
This algorithm works on below 2 steps:
- Subtract 1 from the number will flip all the rightmost set bit.
- and using bitwise & operator with (n) &(n-1) will remove the rightmost set bit from n.
i.e consider 10 in binary is 1 0 1 0
subtract -1
Result = 1001 i.e 9.
When we do (1010 & 1001) we get 1000.
Similarly, we continue like this till we get the count of set bits of number 10.
Method 2:
We can also solve this problem with help of library function available in C++ as below:
bitset<32>(x^y).count();
Solution in C++
#include<iostream>
using namespace std;
int hamming_distance_xor(int x, int y)
{
int count = 0, n = x ^ y;
while (n) {
++count;
n &= n - 1;
}
return count;
}
int hamming_distance_library(int x, int y)
{
return bitset<32>(x^y).count();
}
int main()
{
int num_1 = 8;
int num_2 = 1;
cout<<"Hamming distance using xor is = "<<hamming_distance_xor(num_1, num_2)<<endl;
cout<<"Hamming distance using library function is = "<<hamming_distance_library(num_1, num_2)<<endl;
}
Output:
Hamming distance using xor is = 2 Hamming distance using library function is = 2