Introduction to Isomorphic Graph and understanding with example
In this chapter we shall learn about Isomorphic Graph with example.
Definition:
2 graph G1 and G2 are said to be isomorphic if there exist a match between their vertices and edges such that their incidence relationship is preserved.
For 2 graph to be isomorphic, it should satisfy below properties:
- Same number of vertices.
- Same number of edges.
- Equal number of vertices with given degree.
We shall understand the above definition and properties with the help of an example.
But first, what is incidence relationship?
If two edges e1 and e2 have a common vertex V1, the edges are called incidence relationship.
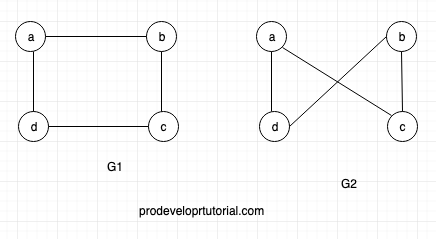
Consider 2 graph below and check if they are isomorphic graph?
First let’s look at the properties:
- They both have same number of edges
- They both have same number of vertices
- All the vertices has same degree.
Now that we shave satisfied the properties, let’s check if they are isomorphic.
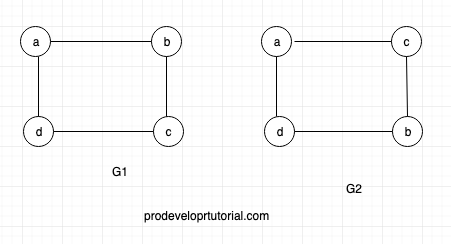
In the graph G2, if we invert the vertex “b” and “c”, then it will equivalent to graph V1 as shown below.
Hence you can see
G1 (a, b) = G2 (a, c)
G1 (a, d) = G2 (a, d)
G1 (d, c) = G2 (d, b)
G1 (b, c) = G2 (c, b)
Hence G1 and G2 are isomorphic.
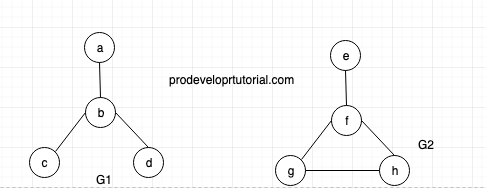
Example 2: Check if the graph is isomorphic.
Here the vertices are 4, but, edges for graph G1 are 3 and for G2 are 4. Hence the 2 graphs are not isomorphic.
Further Reading: