Problem description:
You are given non negative integers “i” represents x axis, and “a[i]” represents y axis. “n” vertical lines are drawn, find two lines together x axis that forms a container. Find the container such that the container will hold the most water.
I understand that the question is difficult to understand, below is the explanation so that it can be understood easily.
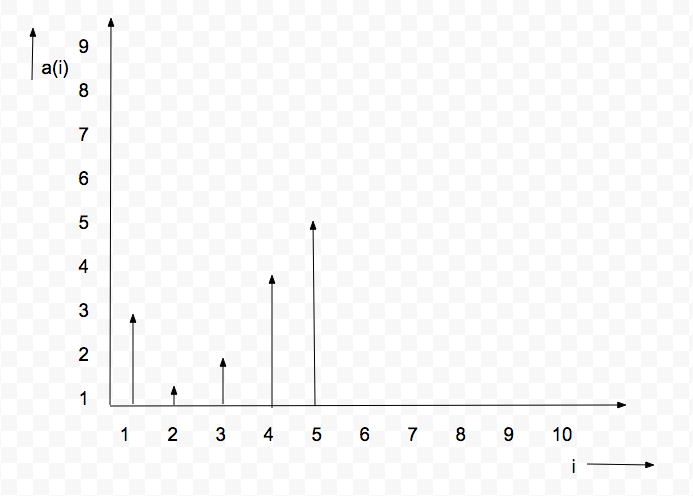
The input array is [3, 1, 2, 4, 5] and can be diagrammatically represented as:
From the diagram it is clear that the horizontal line represents “i” and vertical represents “a(i)”.
Here in this question, we need to find a container that holds most water.
Input: [3, 1, 2, 4, 5] Output: 12
To find the container that holds the most water, we need to calculate the area of all the container, then we have to take the max of all the area.
To find out the area, we use the below formula:
area= (right – left) * min (left_height, right_height)
How did we come up with that formula?
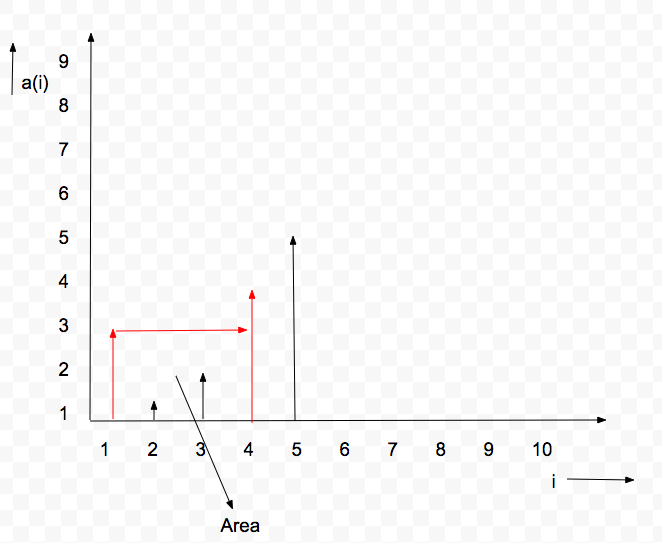
Let us analyze with the help of the diagram below.
From the diagram, the area is determined by the difference between the left and right lines [marked in red]. Since it is a rectangle we need to get the height and width.
Here, height is the minimum of the left_height and right_height. We should not take the max height, because it might overflow.
Width will be the distance between the 2 lines. Hence (right – left).
With the help of the above formula, we get the area.
Then we get the “max_area” by taking the max value of all the possible container area.
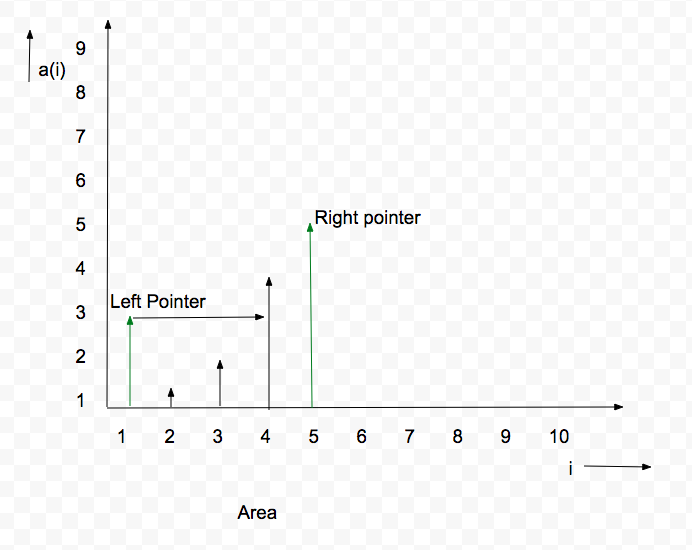
We solve this by taking 2 variables a left_ variable and right_ variable. Left_ variable will start from the beginning and right_ variable will point at the end.
Pseudo code:
while (left_pointer < right_pointer)
{
area = min(arr [left_pointer], arr [right_pointer]) * (right_pointer - left_pointer)
if max_area < area
max_area = area
if (arr[left_pointer] < arr [right_pointer])
left_pointer ++
else
right_pointer ++
}
Pass 1:
left_pointer = 0
right_pointer = 4
max_area = 0
while (left_pointer < right_pointer)
area = min (arr[0], arr[4]) * (4 - 0)
= min (3, 5) * 4
= 12
max_area < area = 0 < 12 true
max_area = 12
if (arr[0] < arr[4]) true
left_pointer ++; i.e left_pointer = 1
end while
Pass 2:
left_pointer = 1
right_pointer = 4
max_area = 12
while (left_pointer < right_pointer)
area = min (arr[1], arr[4]) * (4 - 1)
= min (1, 5) * 3
= 3
max_area < area = 12 < 3 false
if (arr[1] < arr[4]) true
left_pointer ++; i.e left_pointer = 2
end while
Pass 3:
left_pointer = 2
right_pointer = 4
max_area = 12
while (left_pointer < right_pointer)
area = min (arr[2], arr[4]) * (4 - 2)
= min (2, 5) * 2
= 4
max_area < area = 12 < 4 false
if (arr[2] < arr[4]) true
left_pointer ++; i.e left_pointer = 3
end while
Pass 4:
left_pointer = 3
right_pointer = 4
max_area = 12
while (left_pointer < right_pointer)
area = min (arr[3], arr[4]) * (4 - 3)
= min (4, 5) * 1
= 4
max_area < area = 12 < 4 false
if (arr[3] < arr[4]) true
left_pointer ++; i.e left_pointer = 4
end while
Pass 5:
left_pointer = 4
right_pointer = 4
max_area = 12
while condition will fail. Hence max area is 12.
Solution in C++
#include<iostream>
using namespace std;
void calculateMaxContainer(int arr[], int length)
{
int left_pointer = 0;
int rigth_pointer = length -1;
int max_area = 0;
int area = 0;
while (left_pointer < rigth_pointer)
{
// Calculating the max area
// as we have to use constant space of O (1)
// area = min(arr[left_pointer], arr[rigth_pointer]) * (rigth_pointer - left_pointer);
// if (max_area < area)
// max_area = area
// can be written as shown below:
max_area = max(max_area, min(arr[left_pointer], arr[rigth_pointer]) * (rigth_pointer - left_pointer));
if ( arr [left_pointer] < arr [rigth_pointer] )
left_pointer += 1;
else
rigth_pointer -= 1;
}
cout << "The max area is = "<< max_area<< endl;
return ;
}
int main()
{
int a[] = {3, 1, 2, 4, 5};
int length = 5;
calculateMaxContainer(a, length);
}
Output:
The max area is = 12
ayushi maheshwari
can you please provide more test case for all problems