In this tutorial we shall learn about rod cutting problem.
Problem statement:
You are given a rod of length n and you need to cut the cod in such a way that you need to sell It for maximum profit. You are also given a price table where it gives, what a piece of rod is worth.
Example
So, according to the above table, if you cut the rod of length 1 you can see it for 2 rs.
Similarly, if you cut the rod at length 2, you can sell it at 7 rs
Similarly, if you cut the rod at length 3, you can sell it at 10 rs
According to the question, you need to find how to cut the rod so that you get maximum profit.
In our example, the length of the rod is 5.
If you give the whole rod, without cutting it, the profit is 12 rs.
But if you cut the rod at length 3 and length 2, the total profit will be 7 + 10 = 17. This gives us maximum profit.
So, how can you solve this problem?
One method is to use Brute Force approach. In Brute force method, for length n = 4, we get below combinations.
1 1 1 1
1 1 2
1 2 1
2 1 1
3 1
2 2
1 3
4
From above we have total 8 different ways to cut the rod of length 4. Then we need to find the profit of all the combinations and find the max in them. Then we arrive at the result.
But it will take 2^n-1 i.e 2^4-1 = 2^3 = 8 different ways.
Hence the time complexity at worst case will be O(2^n-1).
We can reduce the time complexity to O(n^2) if you use DP.
Let’s see how to apply DP to our problem.
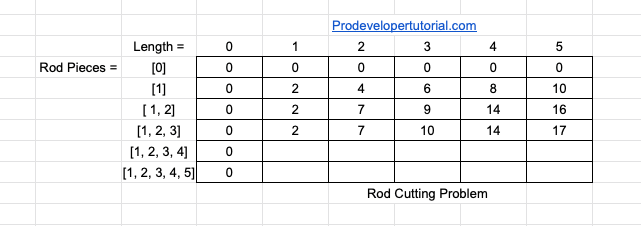
As usual for DP we need a DP matrix. Initial matrix will be as below:
On the row we shall have the length of the rod. On the column we shall have the number of pieces length available to sell.
In the table we shall fill with the profit. At the end we shall receive the max profit.
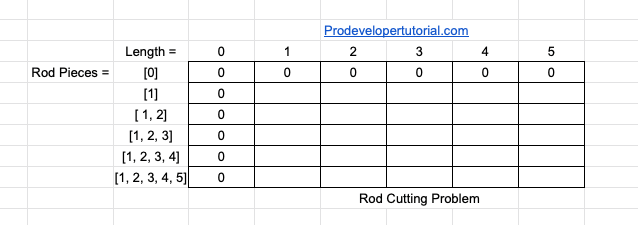
When the rod length is 0, the profit will also be 0.
Hence we can initially fill the matrix as below:
It is important to start every DP matrix from ‘0’, so that you will be clear while solving the sub problem.
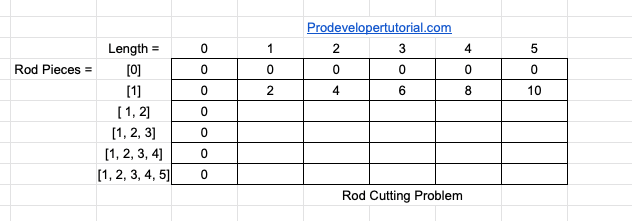
Going to the next row. “row 1”. We have rod piece of length 1. Hence for every varying length, we need to use combinations of rod piece 1 and calculate the profit.
For length 1 the profit will be 2.
For length 2 the profit will be 4.
For length 3 the profit will be 6.
For length 4 the profit will be 8.
For length 5 the profit will be 10.
So, the updated matrix will be as below:
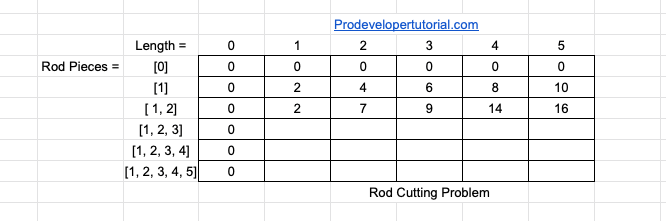
Now for the next row, we have the rod piece combination of [1, 2]. Now we shall fill the array as below.
At length 1, you can use only 1 length. Hence profit is 2.
At length 2, you can have 2 choices. Either you use rod of length 1 twice or rod of length 2 once. As we ned max profit, we calculate the profit in both of the cases.
i.e
1 piece + 1 piece = 2 + 2 = 4
Rod of length 2 = 7.
As we need maximum, we choose 7.
Similarly, for length 3, we can cut the rod for 1 length & 2 lengths. Hence profit is 2 + 7 = 9
Similarly, for length 4, we can cut the rod for 2 length & 2 lengths. Hence profit is 7 + 7 = 14
Similarly, for length 5, we can cut the rod for 2 length & 2 lengths & 1 length. Hence profit is 7 + 7 + 2 = 16
Hence our updated DP table is as below:
Similarly, we shall find for next row. In next row, we have rod choice of length [1, 2, 3].
For length 1, profit is 2.
For length 2, profit is 7. We take both of these values from above.
For length 3, we can cut the rod for 2 length & 1 lengths. Hence profit is 9 or we can sell the whole rod of length 3 for profit 10. We choose the max profit i.e 10.
For length 4, we can cut the rod for 2 length & 2 lengths. Hence profit is 14 or we can cut the rod of length 3 & 1 length for profit 12. We choose the max profit i.e 14.
For length 5, we can cut the rod for 3 length & 2 lengths. Hence profit is 17.
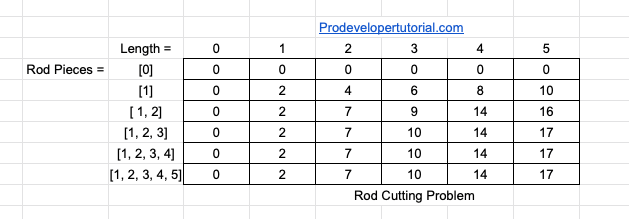
The updated DP table is as below:
By looking at above table we can derive a DP formula? Yes, we can, as below:
For i = 1 to n
For j = 1 to n
If i < j
dp [i] [j] = dp [i-1][j]
else
dp[i][j] = max(dp[i-1][j], arr[i]+dp[i][j-1])
Similarly, we shall solve our matrix.
The final matrix will be as below:
Hence the result.
Solution in C++
#include<iostream>
using namespace std;
int get_max(int a, int b) { return (a > b)? a : b;}
int rod_cutting_dp_solution(int price[], int n)
{
int dp_table[n+1];
dp_table[0] = 0;
int i, j;
for (i = 1; i<=n; i++)
{
int max_val = INT_MIN;
for (j = 0; j < i; j++)
max_val = get_max(max_val, price[j] + dp_table[i-j-1]);
dp_table[i] = max_val;
}
return dp_table[n];
}
int main()
{
int arr[] = {2, 7, 10, 11, 12};
int size = sizeof(arr)/sizeof(arr[0]);
cout<<"Maximum Value is "<< rod_cutting_dp_solution(arr, size)<<endl;
return 0;
}
// Maximum Value is 17